Лекция 2. - матричная экспонента (переходная матрица состояния),

Здесь

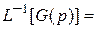
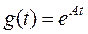- матричная экспонента (переходная матрица состояния),

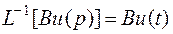- векторная функция.

Состояние x(t) зависит только от начального состояния и входного сигнала. Для нахождения реакции системы подставим в уравнение 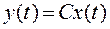(2) выражение (**):

y(t)=y_св(t)+y_вын(t),

где

, .

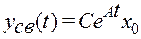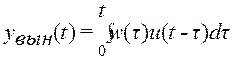Здесь

y_св(t)– свободное движение (движение системы, предоставленной самой себе, за счет ненулевых начальных условий) при u 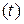=0,

y_вын(t)– вынужденное движение (зависит лишь от свойств системы и входного воздействия) при х₀=0,

матрица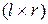

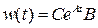
- матричная весовая функция многомерной системы. Если х₀=0, то многомерная система предварительноневозбуждена и

y(t) = y_вын(t).

Если 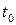не равно нулю, то

.

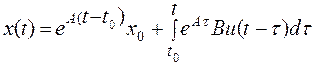В методах, основанных на моделях в переменных состояния, внимание фокусируется на векторе состояния в большей степени, чем на выходе системы. При этом нет особой необходимости различать одномерные и многомерные системы. Это обстоятельство является одним из достоинств методов пространства состояний. Однако нельзя это различие не учитывать при использовании частотных методов.

Свойство резольвенты. Покажем, что резольвенту можно представить как отношение матричного и скалярного полиномов. По определению обратной матрицы:

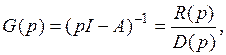
где

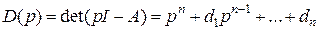
есть характеристический многочлен (полином) матрицы системы А,

.

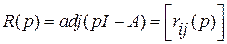есть полиномиальная матрица ( 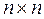), каждый (i, j)-элемент 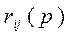которой представляет собой полином не выше степени n-1:

.

(примечание. adjoint- присоединенная матрица, т.е. алгебраическое дополнение матрицы ( )).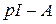

Следовательно, матрицу R(p) можно трактовать как матричный полином

,

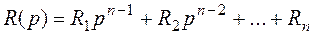где 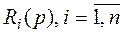- постоянные матрицы ( ).

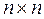Пример. Для n=2

.

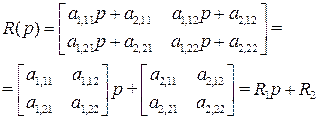Отсюда резольвенту можно представить в виде отношения матричного полинома R(p) и характеристического полинома (скалярного) D(p):

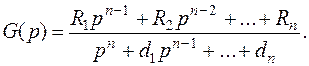
Полагая известными собственные значения s_i матрицы А, другими словами, корни характеристического уравнения системы D(p) =0, и считая, что все корни простые, получаем

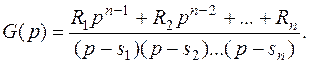
Разлагая на простые дроби, находим

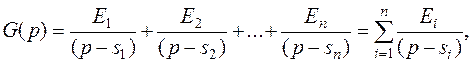
где E_i – неопределенные матричные коэффициенты.

Находя обратное преобразование Лапласа, получаем выражение

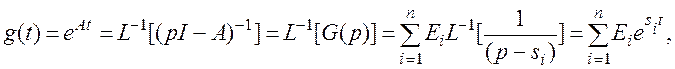
связывающее переходную матрицу состояния и корни характеристического уравнения системы.