Определение реакции линейной многомерной управляемой системы с помощью преобразования Лапласа.
Одной из важных задач анализа является определение реакции многомерной управляемой системы на входной сигнал.
Дано: Модель типа «вход – состояние – выход»
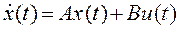 , (1)
, (1)
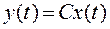 . (2)
. (2)
Известно управление u (t) для t>t0 и начальное состояние x(t0)=x0.
Найти: Выходной сигнал у(t), t>t0.
Решим эту задачу с помощью преобразования Лапласа. Пусть t0=0.
Преобразуем по Лапласу уравнение (1). Все теоремы о преобразовании Лапласа скалярных величин справедливы и для векторных величин.
Используя теорему линейности, получаем
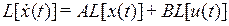 .
.
Обозначим преобразование Лапласа вектора состояния 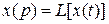 и преобразование Лапласа управления
и преобразование Лапласа управления 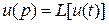 .
.
Используя теорему об изображении производной
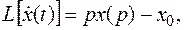
получаем
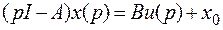 , (*)
, (*)
где I – единичная матрица ( 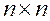 ).
).
Введем в рассмотрение резольвенту 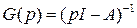 , матрицу (
, матрицу ( 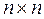 ). Умножая слева уравнение (*) на резольвенту, получаем изображение по Лапласу вектора состояния
). Умножая слева уравнение (*) на резольвенту, получаем изображение по Лапласу вектора состояния
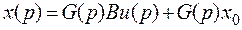 .
.
Определяя обратное преобразование Лапласа, находим решение уравнения (1):
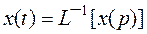 .
.
Если учтем, что 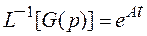 - матричная экспонента и воспользуемся теоремой об изображении свертки двух функций, получим
- матричная экспонента и воспользуемся теоремой об изображении свертки двух функций, получим
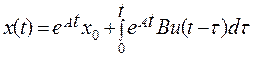 . (**)
. (**)
Дата добавления: 2015-08-14; просмотров: 1074;
