В переменных состояния.

Лекция 1

Математические модели систем управления

в переменных состояния.

В данном разделе представлены математические модели систем управления в переменных состояния.

1.1. Уравнения линейных управляемых систем в переменных состояния.

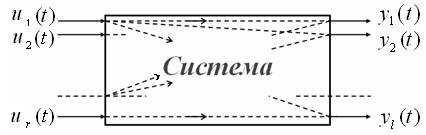Объекты управления, приводимые управляющими устройствами в желаемое состояние, являются непрерывными динамическими системами, которые в общем случае имеют r управляющих воздействий (входов) 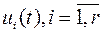и l управляемых величин (выходов) 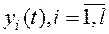.(рис.1). Поэтому ОУ называют также управляемыми системами.

Системы с несколькими выходами и несколькими входами 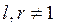называют многосвязными (многомерными, MIMO). Если 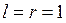, то система имеет один вход 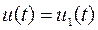и один выход 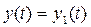и определяется как односвязная (одномерная , SISO) система. Таким образом, односвязную систему можно рассматривать как частный случай многосвязной системы и поэтому к описанию этих систем можно подходить с единых позиций.

Многомерные линейные системы описываются системой дифференциальных уравнений, каждое из которых имеет тот или иной порядок. Для целей анализа и синтеза систем удобно нормализовать эту систему уравнений и записать ее в виде системы дифференциальных уравнений первого порядка, разрешенных относительно первых производных, т. е. уравнений в форме Коши:

, ( * )

, (**)

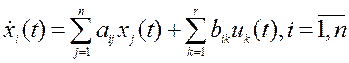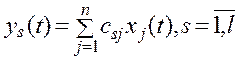где 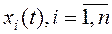носят название переменных состояния, коэффициенты 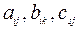- некоторые постоянные, n – порядок системы. Здесь уравнение (**) представляет собой систему из l алгебраических уравнений. При постоянных коэффициентах 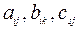управляемая система называется стационарной системой (системой с постоянными параметрами). Если хотя бы один из этих коэффициентов зависит от времени, то управляемую систему называют нестационарной системой (системой с переменными параметрами).

Состояние управляемой системы – необходимая и достаточная информация для определения будущих значений ее выходного сигнала по уравнениям типа «вход-состояние-выход» (модели системы) при заданном входном сигнале.

Обычно ( * ) и (**) , т.е. уравнения типа «вход-состояние-выход», записывают в векторно-матричной форме:

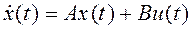, (1)

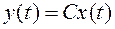, (2)

где вектор 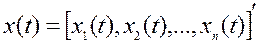называется вектором состояния, вектор - вектором входа, вектор - вектором выхода. Штрихом обозначена операция транспонирования.

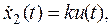(4)

Векторная форма уравнений двойного интегратора в развернутом виде выглядит так

.

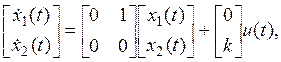
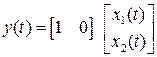Сопоставляя полученные выражения с уравнениями (1) и (2), находим

.

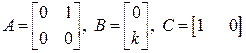Заметим, что в данном случае n=2, .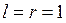

Примером объекта, описываемого уравнением интегратора второго порядка, является спутник, схематическое изображение которого изображено на рис. ниже.

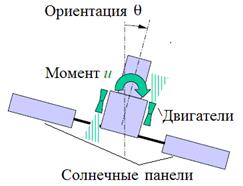
Предполагается, что спутник жесткий и что он вращается вокруг оси, перпендикулярной странице конспекта. Вращающий момент, прикладываемый к спутнику, создается двигателями. Если двигатели включены так, как показано на рисунке, это приводит к увеличению угла ориентации 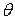. Предполагается, что момент u(t), создаваемый двигателями, является входом объекта, а угол ̶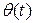 его выходом. Тогда в соответствии со вторым законом Ньютона

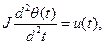
поскольку трение о воздух отсутствует (J ̶ момент инерции двигателя).

Это достаточно точная модель спутника, и она часто используется во многих приложениях. Однако если к спутнику прикреплены солнечные панели, то допущение о его жесткости уже не действует (одни части спутника могут перемещаться относительно других частей) и модель получается более сложной.

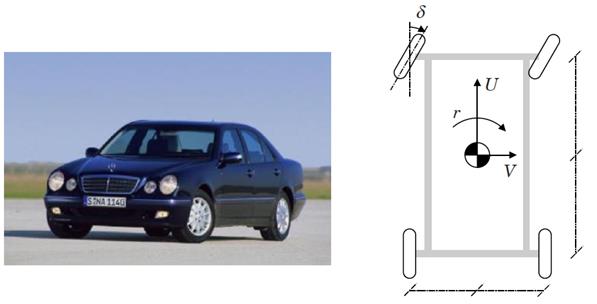
Пример 2. Управление динамикой автомобиля. Обратная связь используется для повышения безопасности путем управления торможением, чтобы прдотвратить заклинивание колес, и предотвратить скольжение на мокрой дороге.

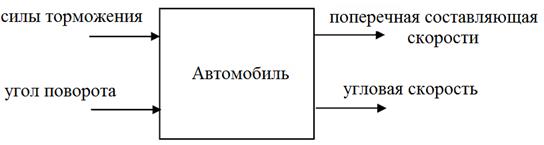
Упрощенная модель динамики автомобиля дается уравнениями

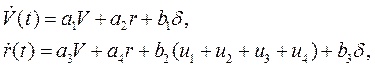
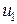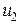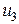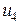где V есть поперечная составляющая скорости и r есть угловая скорость. Имеется пять управляющих воздействий, угол поворота и силы торможения , , , на четыре колеса. Схематическое изображение такого объекта приведено на рис. ниже.

Команды Matlab: ss, ss2tf, tf2ss.

Например, Gtf=tf([1, [1 2 3]); Gss=ss(Gtf).

Для систем управления, описание которых представлено в переменных состояния, решение многих задач облегчается путем применения цифровых компьютеров.