Булевы функции двух переменных.
 Пусть х1 и х2 — логические переменные. Рассмотрим функцию от х, и х2:
Пусть х1 и х2 — логические переменные. Рассмотрим функцию от х, и х2:
f(х1,х2). (11.8)
Так как каждая из переменных х1, х2 может принимать только два значения: 0 и 1,
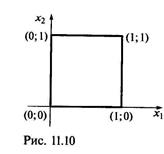
то областью определения функции (11.8) являются четыре варианта сочетаний: 00, 01, 10 и 11. Приняв эти сочетания за координаты точек на плоскости х1Ох2, получим четыре вершины единичного квадрата (рис. 11.10). Таким образом, функцию (11.8) можем считать заданной на множестве вершин единичного квадрата, и это множество она отображает во множество {0, 1}. Например, функция f(х1, х2) может быть равна единице во всех вершинах, кроме начала координат, а в начале координат обращаться в нуль.
Легко найти общее число всевозможных функций f(хь х2) со значениями в 0, 1}. В самом деле, перенумеруем вершины единичного квадрата в каком-нибудь порядке. В каждой вершине функция f(х1,, х2) может принимать одно из двух значений: 0 или 1. Задать функцию — значит указать, в каких вершинах она принимает значение 0 и в каких 1. Таким образом, наша функция — это четырехбуквенное слово, образованное из алфавита {0, 1}. Число таких слов равно 24= 16. Следовательно, можно построить только 16 различных функций двух логических переменных со значениями в {0, 1}. Перечислим эти функции.
| Таблица 11.11 | Таблица 11.12 | ||||||||
| х1 | х2 | f(х1,х2)=0 | х1 | х2 | f(х1,х2)=1 | ||||
| Таблица 11.13 | Таблица 11.14 | ||||||||
| х1 | х2 | f(х1,х2)= х1 | х1 | х2 | f(х1,х2)= х2 | ||||
| Таблица 11.15 | Таблица 11.16 | |||||||
| х1 | х2 | f(х1,х2)= 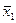
| х1 | х2 | f(х1,х2)= 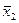
| |||
| Таблица 11.17 | Таблица 11.18 | ||||||||
| х1 | х2 | х1 Ùх2 | х1 | х2 | х1Úх2 | ||||
Прежде всего отметим две простейшие функции — постоянные: f(х1,х2)=0 и f(х1,х2)= 1 (табл. 11.11 и 11.12).
Еще две тоже очень простые функции f(х1,х2)= х1 и f(х1,х2)= х2 (табл. 11.13 и 11.14). Аналогично строятся функции f(х1,х2)= 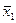 , и f(х1,х2)=
, и f(х1,х2)= 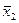 (табл. 11.15 и 11.16).
(табл. 11.15 и 11.16).
Все эти функции уже встречались при рассмотрении функции одной логической переменной. Перейдем теперь к более интересным функциям двух логических переменных.
Конъюнкция.Так называется функция f(х1,х2), которая принимает значение, равное единице, тогда и только тогда, когда оба аргумента равны 1 (табл. 11.17). Конъюнкция обозначается х1Ùх2 или х1 ,х2, читается «х1 и х2» (Иногда конъюнкцию обозначают знаком &. До сих пор не установилось единое обозначение и для других функций. Так, например, для отрицания существуют еще два знака). Легко видеть, что конъюнкцию можно определить также равенством х1Ùх2 = min(х1|, х2). Таким образом, чтобы конъюнкция была равна нулю, необходимо (и достаточно), чтобы хоть один аргумент был равен нулю.
Дизъюнкция. Так называется функция f(х1,х2), которая принимает значение 0 тогда и только тогда, когда оба аргумента равны 0 (табл. 11.18). Дизъюнкция обозначается х1Úх2, и читается «х1 или х2». Легко видеть, что дизъюнкцию можно определить равенством х1Úх2, = mах(х1, х2). Таким образом, чтобы дизъюнкция была равна единице, достаточно (и необходимо), чтобы хоть один из аргументов был равен единице.
Вопросы для контроля знаний и подведения итога прочитанной лекции
1. Что называют отрицаниемвысказывания р?
2. Что называют конъюнкциейдвух высказываний р и q?
3. Что называют дизъюнкциейдвух высказываний р и q?
4. Что называют импликацией двух высказываний р и q?
5. Что называют эквиваленциейдвух высказываний р и q?
Дата добавления: 2015-08-20; просмотров: 1353;
