Булевы функции

1. Булевы функции одной переменной. Будем, как обычно, обозначать независимую переменную символом х. Если независимых переменных несколько, будем их нумеровать: х₁,х₂, ..., х_n.

Рассмотрим возможные функции от переменной х ÎD = {0, 1} (такая переменная называется логической переменной). При этом нас будут интересовать лишь те функции, значения которых лежат также в D= {0, 1}. Таких функций не много. В самом деле, можно указать, например, степенную функцию: f(х) = хⁿ. Но эта функция в данном случае ничем не отличается от тождественной функции f(х) = х, так как значение 0 она переводит в 0, а значение 1 в 1. Построим таблицу функции f(х) = х (табл. 11.7), для чего слева перечислим значения аргумента (0 и 1), а справа — соответствующие значения функции.

Другой более интересной функцией является отрицание. Эта функция обозначается х и читается «не х». Она действует следу­ющим образом: если х = 0, то 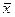= 1, и наоборот, если х = 1, то 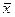= 0 (табл. 11.8).

Таблица 11.7		Таблица 11.8		Таблица 11.9		Таблица 11.10
x	f(х) = х		х	f(х) =	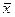	x	f(х) = 1		х	f(х) = 0

Кроме этих двух функций можно указать еще только две функции, отображающие множество {0, 1} в себя. Это постоянные f(х) = 1 и f(х) = 0 (табл. 11.9 и 11.10).

Других функций от одной логической переменной, отображающих {0, 1} в себя, не существует. В самом деле, любая такая функция определяется двумя значениями (f (0) и f (1)), причем каждое из этих значений может быть равно либо 0, либо 1. Таким образом, каждая такая функция — это двухбуквенное слово f (0) f (1), образованное из {0, 1}, как из алфавита. Число таких слов, а следовательно, и число интересующих нас функций, равно, как мы знаем, 2² = 4. Ровно столько функций мы и перечислили, а все возможные двухбуквенные слова, которые можно образовать из {0, 1}, записаны в правых частях таблиц (см. табл. 11.7—11.10).

Итак, если x: — логическая переменная, то существует только четыре функции f(х), отображающие область определения D = {0, 1} в себя: две постоянные, одна тождественная и одна — отрицание. Эти функции называют булевыми функциями одного переменного (Джон Буль (1815— 1864) — английский ученый..Каждую из этих функций можно задать аналитически, т.е. с помощью формул, например f(х) = х, или таблично.

Заметим еще, что так же, как в непрерывном анализе, одну и ту же функцию можно задать с помощью разных формул. Например, функциюf(х) = 0 можно задать и формулой f(х) = .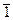

Имея всего четыре функции, трудно построить исчисление, столь же содержательное, как анализ непрерывных функций. Перейдем поэтому к изучению функций, зависящих от нескольких логических переменных, значения которых лежат в D = {0, 1}. Такие функции называют булевыми функциями нескольких переменных. В этом случае также получим конечное множество функций, но запас их достаточно велик, чтобы построить содержательный математический аппарат.