Высказывания
1. Понятие высказывания. Предложение, о котором имеет смысл говорить, что оно истинно или ложно, называется высказыванием.
Высказываниями являются, например, следующие предложения: «3x3 = 9», «7 — простое число», «Волга впадает в Черное море». Первые два предложения истинны, а третье — ложно.
Существуют предложения, относительно содержания которых в настоящий момент неизвестно, истинно оно или ложно. Так, например, предложение «Существуют внеземные цивилизации» является высказыванием несмотря на то, что в настоящее время неизвестно, существуют ли в действительности внеземные цивилизации. Однако ясно, что это утверждение либо истинно, либо ложно, поэтому оно является высказыванием. Предложение «В романе Л.Н. Толстого "Война и мир" 3851385 букв» также является высказыванием, хотя, вероятно, никто не знает, истинно оно или ложно (но абсолютно точно известно, что оно либо истинно, либо ложно).
Единственным существенным признаком высказывания является то, что оно либо истинно, либо ложно, но не может быть истинным и ложным одновременно.
Обычно высказывания обозначают маленькими буквами латинского алфавита: р, q, х, у и т.д.
Не всякое предложение является высказыванием. Так, предложения «Который час?», «Да здравствуют музы!» (как и всякие вопросительные или восклицательные предложения) не являются высказываниями.
В логике высказываний интересуются не содержанием, а истинностью или ложностью высказываний (т.е. их истинным значением). Истинностные значения — истина и ложь — будем обозначать соответственно И и Л.
Грамматическими средствами в разговорном языке из нескольких простых высказываний можно составить сложное (составное) высказывание. Например, с помощью союзов «и», «или» и частицы «не» можно из простых высказываний «Москва стоит на берегу Оби» (ложного) и «Новосибирск стоит на берегу Оби» (истинного) составить следующие сложные высказывания: «Москва не стоит на берегу Оби», «Москва стоит на берегу Оби или Новосибирск стоит на берегу Оби», «Москва стоит на берегу Оби и Новосибирск стоит на берегу Оби». Первые два высказывания истинны, а последнее — ложно.
2. Операции над высказываниями. Рассмотрим логические операции над высказываниями, при которых истинностные значения составных высказываний определяются только истинностными, значениями составляющих высказываний, а не их смыслом.
Отрицаниемвысказывания р называется высказывание, истинное тогда и только тогда, когда высказывание р ложно.
Отрицание р обозначается через 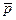 и читается как «не р». Отрицание высказывания определяется также таблицей истинности (табл. 11.1 или 11.2).
и читается как «не р». Отрицание высказывания определяется также таблицей истинности (табл. 11.1 или 11.2).
| Таблица 11.1 | Таблица 11.2 | |||
| p | 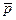
| p | 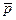
| |
| Л | И | или | ||
| И | Л |
Здесь цифрами 1 и 0 обозначены соответственно истинность и ложность высказывания.
Конъюнкциейдвух высказываний р и q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания.
Конъюнкция высказываний р и q обозначается через р Ù q и читается так: «р и q». Конъюнкция определяется также таблицей истинности (табл. 11.3).
В разговорной речи конъюнкции соответствует соединение высказываний союзом «И».
Дизъюнкциейдвух высказываний р и q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны.
Дизъюнкция высказываний р и q обозначается через р Ú q и читается как «р или q». Дизъюнкция определяется также таблицей истинности (табл. 11.4).
| Таблица 11.3 | Таблица 11.4 | ||||||
| p | q | pÙq | p | q | pÚq | ||
| Таблица 11.5 | Таблица 11.6 | ||||||
| p | q | p®q | p | q | p~q | ||
В разговорной речи дизъюнкция соответствует соединению высказываний союзом «или» в неразделительном смысле.
Импликациейдвух высказываний р и q называется высказывание, ложное тогда и только тогда, когда р истинно, а q ложно.
Импликация высказываний р и q обозначается через р ® q читается как «р влечет q» (или иначе, «если p, то q», «из р следует q»). Высказывание р называется посылкой импликации, а высказывание р — заключением импликации. Импликация определяется также таблицей истинности (табл. 11.5).
Эквиваленцией (или эквивалентностью) двух высказываний р и q называется высказывание, истинное тогда и только тогда, когда истинностные значения р и q совпадают.
Эквиваленция высказываний р и q обозначается через р ~ q и читается как «р эквивалентно q». Эквиваленция определяется также таблицей истинности (табл. 11.6).
3. Прямая и обратная теоремы. В каждой теореме должно быть указано:
1) при каких условиях рассматривается в ней тот или иной математический факт (условие теоремы);
2) что об этом факте утверждается (заключение теоремы), Рассмотрим, например, следующую теорему.
Теорема 11.6. Если четырехугольник — параллелограмм, то его диагонали, пересекаясь, делятся пополам.
Здесь условие теоремы (р): четырехугольник — параллелограмм; заключение теоремы (q): точка пересечения диагоналей делит каждую из них пополам.
Чтобы легче выделить условие и заключение теоремы, ее часто формулируют в виде импликации, применяя логический союз «если ... , то ...». Поэтому теорему можно записать в общем виде на языке логики так: p®q..
Доказательство теоремы состоит в том, чтобы показать, что если выполняется условие, то из него логически следует заключение, т.е. приняв, что р истинно, в соответствии с определенными правилами логики показать, что q истинно.
Имея некоторую теорему p®q, из нее можно образовать новую теорему q® р, называемую обратной к теореме p®q. В этом случае исходная теорема называется прямой теоремой.
Например, обратной теоремой к приведенной выше теореме 11.6 является следующая теорема.
Теорема 11.7. Если в четырехугольнике диагонали, пересекаясь, делятся пополам, то этот четырехугольник — параллелограмм.
В данном примере теоремы 11.6 и 11.7 истинны, в чем легко убедиться, проводя доказательство каждой из них.
Однако из справедливости теоремы p®q не всегда следует справедливость теоремы q® р. Так, справедливо предложение «Если углы вертикальные, то они равны» (p®q), но неверно, что «Если углы равны, то они вертикальные» (q® р). Например, прямые углы равны, но они необязательно будут вертикальные.
4. Необходимое и достаточное условия.
Пример 11.5. Рассмотрим следующие высказывания.
1) Если данное натуральное число четное, то оно делится на шесть.
2) Если данное натуральное число делится на шесть, то оно четное.
3) Если данное натуральное число четное, то оно делится на два.
4) Если данное натуральное число делится на два, то оно четное.
Каждое из этих высказываний можно выразить на языке математической логики:
1) p1®q1; 2) q1® p1; 3) p2®q2; 4) q2® p2.
Первое высказывание не является истинным, второе, третье и четвертое высказывания истинны.
Формулируя теорему, часто используют термины «достаточно», «необходимо», «достаточно и необходимо».
Условие p называется достаточным для заключения q, если из p логически следует q, т. е. истинна теорема p®q.
Условие р называется необходимым для заключения q, если из q логически следует p1®q1, т.е. истинна теорема q ® p..
Условие р называется достаточным и необходимым для заключения q, если из р логически следует q, а из q логически следует р, т. е. истинны обе теоремы: прямая и ей обратная.
В рассмотренном выше примере р1не является условием, достаточным для q1, так как из р1, логически не следует q1,,т. е. из истинности р1, не вытекает истинность q1, р2 является достаточным условием для q2, т. к. из р2 логически следует q2..
Вместе с тем р1 является условием, необходимым для q1ь так как из q1 логически следует р1. Условие р2 есть условие, достаточное и необходимое для q2., так как истинны одновременно обе теоремы: p2®q2 и q2® p2, т.е. имеет место р2 ~ q2..
Возможны случаи, когда:
а) условие р является достаточным для заключения q, но не является необходимым;
б) условие р является необходимым для заключения q, но не является достаточным.
В случае а) из истинности р вытекает истинность q, но истинность q может вытекать и из другого условия. Например, чтобы число было четным, достаточно не только того, что оно делится на шесть, но и того, что оно делится на четыре.
В случае б) из истинности q вытекает истинность p, однако, если р будет истинно, то q все же может оказаться ложным. Например, чтобы число делилось на шесть, необходимо, но недостаточно, чтобы оно было четным; так, число четыре четное, однако оно не делится на шесть.
При употреблении терминов «достаточно», «необходимо», «необходимо и достаточно» вместо слова «условие» часто употребляют слово «признак».
Вместо слов «достаточно и необходимо» часто употребляют также словосочетания: «если и только если», «тогда и только тогда», «в том и только в том случае», «те и только те». Полезно иметь в виду, что рассматриваемые отдельно части этих связок также имеют определенный смысл: например, словосочетания «только в том случае», «только тогда» и т. п. заменяют словосочетание «необходимое условие», а словосочетания «тогда», «в том случае» и т. п. заменяют словосочетание «достаточное условие».
Дата добавления: 2015-08-20; просмотров: 1316;
