Понятие высказывания. Составные высказывания

Математическая логика представляет собой формальный математический аппарат, изучающий различные способы логических рассуждений. Простейшую из формальных логических теорий называют алгеброй высказываний.

Высказывание- это утверждение или повествовательное предложение, о котором можно сказать, что оно истинно (И-1) или ложно (Л-0), но не то и другое одновременно.

Например, «Сегодня идет дождь», «Иванов выполнил лабораторную работу №2 по физике».

Истинность или ложность, приписываемые некоторому утверждению, называются его истинностным значением. Характеристика высказывания по признаку истинности называется семантической.

Высказывания, истинные в одних логических ситуациях и ложные в других, называют переменными высказываниями.

Высказывание, истинное во всех случаях, называется логически истинным, или тавтологией. Теоремы в математике являются примерами тавтологий. Было бы неприятно сознавать, что математические теоремы справедливы, к примеру, только в 80% случаев. Каждое высказывание вида 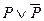- тавтология. Например: «Быть или не быть».

Высказывание, построенное так, что оно ложно в любом случае, называется логически ложным, или противоречием.

Например, высказывание: «Она движется в направлении Самары и она не движется в направлении Самары» всегда ложно, т.к. нельзя делать одновременно и то, и другое, следовательно, это противоречие.

Высказывания обычно обозначаются буквами латинского алфавита. Для высказывания важно его истинное значение, а не смысл предложения. Из высказываний с помощью логических связок образуются новые высказывания.

Высказывание, не содержащее связок, называется простым. Высказывание, содержащее связки, называется сложным. Истинность сложного высказывания однозначно определяется истинностью или ложностью составляющих его частей. Роли связок играют логические операции. Действия логических операций задаются таблицами истинности, каждой строке которых отвечает взаимнооднозначный набор значений элементарных высказываний и соответствующие значения составных. Рассмотрим некоторые логические связки (логические операции).