Логические операции. Отрицанием высказывания Р является новое высказывание, которое является истинным, если высказывание Р ложно и наоборот

Отрицанием высказывания Р является новое высказывание, которое является истинным, если высказывание Р ложно и наоборот. Обозначается 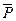. Читается «не Р», «неверно, что Р». Все логические значения высказывания описаны с помощью таблицы 1. Можно образовать 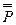- двойное отрицание высказывания Р. Логические значения 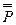совпадают со значениями Р.

Таблица 1

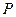
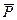
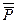
Конъюнкция (логическое умножение двух высказываний) – это новое высказывание R, которое истинно только тогда, когда оба высказывания истинны, и ложно, когда хотя бы одно из них ложно. Обозначается P & Q, 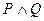, P · Q или PQ. Читается: «P и (а, но, однако, хотя и т.д.) Q». Таблица истинности конъюнкции дана в таблице 2.

Таблица 2

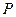
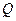
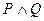
Союз «и» в алгебре логики используется в том же смысле, что и в повседневной речи. Однако в алгебре логики этой связкой можно связывать любые, сколь угодно далекие по смыслу высказывания. Например, «Луна сделана из зеленого сыра, и дронт вымер».

Дизъюнкцией (логическим сложением) двух высказываний P и Q называется новое высказывание, которое истинно, если хотя бы одно из высказываний истинно, и ложно, если оба ложны. Обозначается 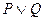. Читается «P или Q». Логические значения дизъюнкции приведены в таблице 3.

Таблица 3

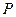
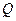
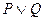
В повседневной речи союз «или» употребляется в различном смысле: исключающем или неисключающем. В алгебре логики связка 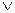употребляется в неисключающем смысле. Например, «Виктор купил автомобиль, или у Ивана светлые волосы».

В исключающем смысле употребляется итерация, которая называется «строгая дизъюнкция (разделительное или)». Обозначается 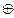. Например, «Анна полетит в Москву самолетом, или она поедет на поезде (Нельзя одновременно лететь на самолете, или ехать на поезде)», «Сегодня понедельник или вторник». Таблица истинности для строгой дизъюнкции совпадает с таблицей истинности логической операции «сложение по модулю два» в булевой алгебре. Таблица истинности операции приведена в таблице 4.

Таблица 4

P	Q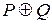

Как видно из таблицы 4, сложное высказывание при использовании строгой дизъюнкции истинно только тогда, когда истинно лишь одно из высказываний.

Импликацией (логическим следованием) двух высказываний P и Q называется новое высказывание, которое ложно, когда P истинно, а Q ложно, и истинно во всех остальных случаях. Обозначается 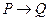. Читается «если P, то Q» или «из P следует Q». Высказывание P является условием, посылкой, а высказывание Q – следствием, заключением. Например, если 2<5, то 7-8=11. Таблица истинности операции – это таблица 5.

Таблица 5

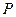
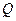
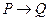
Употребление союзов «если ... то» в алгебре логики отличается от употребления их в обыденной речи, где, как правило, считается, что если P ложно, то Q вообще не имеет смысла. Кроме того, в обыденной речи подразумевается, что из предложения P всегда вытекает Q. В математической логике этого не требуется, т.к. смысл высказываний игнорируется, учитывается только семантическая характеристика.

Эквиваленцией (логической эквивалентностью, эквивалентностью) двух высказываний P и Q называется новое высказывание, которое истинно, когда оба высказывания P и Q либо истинны, либо ложны одновременно, и ложно в остальных случаях. Обозначается 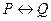. Читается «для того, чтобы P, ... необходимо и достаточно, чтобы Q», или «P – тогда и только тогда, когда Q». Эквивалентность играет большую роль в математических доказательствах: большое количество теорем формируется в форме необходимых и достаточных условий. Логические значения операции эквиваленция приведены в таблице 6.

Таблица 6

P	Q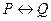

Символы 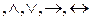называются пропозициональными связками или связками исчисления высказываний. Вместо знака ↔ часто пишут ~ или 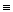, вместо → употребляют 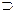, вместо & или 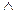часто ставят точку, причем точку иногда опускают, вместо «−» употребляют знак 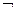или ┐ перед высказыванием.

Не следует думать, что набором отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция исчерпываются все логические связки. Вышеперечисленные операции используются в логике высказываний. В булевой алгебре будут изучены операции штрих Шеффера │, стрелка Пирса ↓. Свои названия эти связки получили в честь математиков Г. Шеффера и Ч. Пирса. Этим связкам соответствуют

таблицы истинности 7 и 8.

Таблица 7	Таблица 8
P Q │	P Q

Из анализа таблиц истинности можно сделать вывод, что операция Штрих Шеффера – это антиконъюнкция, а Стрелка Пирса – это антидизъюнкция.