Лекция 5. 2. Наблюдаемость системы.

2. Наблюдаемость системы.

Определение. Система, описываемая уравнениями в переменных состояния

,

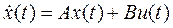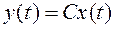, (4)

где x(t) – n-вектор, u(t) – r-вектор, y(t) – l-вектор, называется полностью наблюдаемой, если существует такой момент времени, при котором знания измеренных управляемой величины y(t)иуправляющего воздействия u(t) достаточно для определения начального состояния системы x(0).Это свойство дает возможность восстанавливать начальное состояние x(0),зная u(t) и y(t) для t>0.

Другое определение наблюдаемости. Состояние x₀ 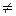0, называется ненаблюдаемым, если при заданных x(0)=x₀ и u(t)=0, 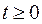, управляемая величина тождественно равна нулю, т.е. y(t)=0, 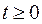. Система называется наблюдаемой, если в ней отсутствуют ненаблюдаемые состояния.

Теорема Калмана. (О наблюдаемости)

Для полной наблюдаемости системы (4) необходимо и достаточно, чтобы матрица наблюдаемости Q имела ранг, равный n.

Матрица наблюдаемости имеет вид:

.

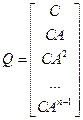Условие полной наблюдаемости:

,

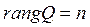где n – порядок системы. Каждый из блоков матрицы Q имеет размерность 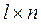, следовательно, матрица Q имеет размерность .

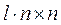Если l=1, то Q – квадратная матрица и условие полной наблюдаемости:

.

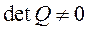Следовательно, система при l=1полностью наблюдаема, если Q – невырожденная матрица.

Пример. Двойной интегратор с матрицами

.

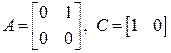Как видим, n=2, .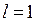

Матрица наблюдаемости:

.

Итак,

,

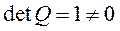то есть двойной интегратор является полностью наблюдаемым.

Физический смысл свойства полной наблюдаемости заключается в том, что при этом каждая из переменных состояния оказывает влияние на управляемую величину. Тогда измеряя y(t), можем судить, как изменяется каждая переменная состояния.

Свойство наблюдаемости является внутренним свойством системы и не зависит от способа ее описания.

Замечание. Система, описываемая уравнением (1), называется обнаруживаемой, если ее неуправляемая часть является наблюдаемой. Это свойство позволяет обнаружить, содержит ли объект управления неустойчивую неуправляемую часть.

Система с одним входом и одним выходом является как полностью управляемой, так и полностью наблюдаемой, если ее ПФ не содержит одинаковых сомножителей в числителе и знаменателе.