Управляемость линейных импульсных систем

Запишем систему разностных уравнений, описывающих объект:

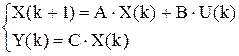
Рис. 3.2

Определение: объект управляем, если для любой пары начальных и конечных состояний существует конечное управляющее воздействие, которое на конечном интервале времени переводит объект из заданного начального состояния в заданное конечное, т.е. существует последовательность:

,

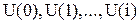пусть i=n-1

Рассмотрим задачу анализа управляемости одноканального объекта:

.

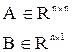Сформируем матрицу управляемости

.

Критерий. Одноканальный объект управляем если матрица Г невырожденная.

det Г¹0.

Доказательство. В соответствии с разностным уравнением объекта можно записать:

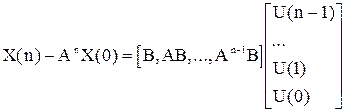
Таким образом последовательность управляющих воздействий переводящих объект из заданного начального состояния в заданное конечное находим следующим образом:

,

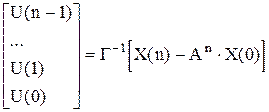откуда и следует требование невырожденности Г.