Наблюдаемость линейных импульсных систем

Запишем разностные уравнения объекта:

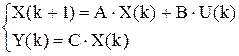
Пусть известно измеренное значение выхода и известна последовательность управляющих воздействий:

,

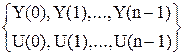по этим данным необходимо найти X(k).

Определение. Объект наблюдаем, если по процессу Y(k) можно вычислить процесс X(k).

Матрицей наблюдаемости для одноканального объекта называется матрица вида:

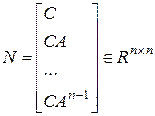, для одноканального объекта.

Критерий. Одноканальный объект наблюдаем, если матрица N невырожденная:

det N¹0.

Доказательство. Воспользуемся уравнением выхода:

Здесь неизвестным является X(0), все остальные величины известны либо измеряемы. Запишем последние уравнения в матричной форме:

.

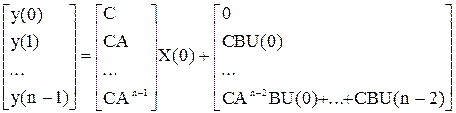Из последней системы уравнений выразим X(0):

.

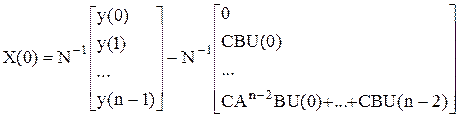Как видим, решение для X(0) существует только, если матрица N не вырожденная. Для оценки вектора состояния X(0) придется набирать информацию о выходе объекта за n шагов, начиная с нулевого.