Астатическая процедура

Если необходимо обеспечить ошибку в системе равной нулю, то используется астатическая процедура синтеза.

Передаточная функция дискретного интегратора имеет вид:

,

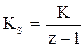K - свободный коэффициент.

Корректор динамики имеет передаточную функцию вида:

,

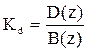dim D(z)=n-1,

,

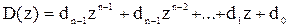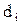- свободные коэффициенты, подлежащие вычислению.

Выведем основные соотношения метода:

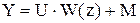
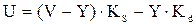
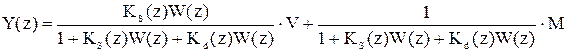
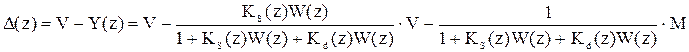
Подставим вместо K_s(z) его передаточную функцию:

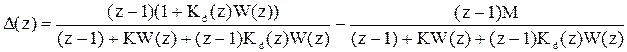
В статике k ® ¥, z ® 1 и, как видно из последнего равенства, ошибка в установившемся режиме будет равна нулю при любом входе и возмущении.

Рассмотрим характеристическое уравнение замкнутой системы:

,

,

.

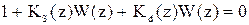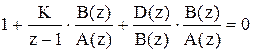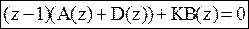Порядок характеристического уравнения системы равен (n+1), т.е. необходимо задать (n+1) желаемый корень. Для этого по желаемому виду переходного процесса найдем желаемую непрерывную передаточную функцию, а от неё посредством Z-преобразования перейдём к желаемой дискретной пердаточной функции:

,

,

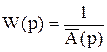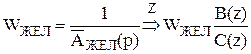
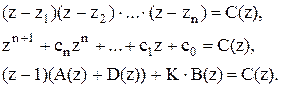
Последнее равенство и есть основное рабочее соотношение для нахождения искомых параметров корректоров статики и динамики.

Передаточную функцию объекта до начала синтеза следует обязательно отнормировать стандартным образом.

Приравнивая коэффициенты при одинаковых степенях z, получаем систему из (n+1) уравнения для нахождения 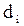и K.

Отметим, что полный порядок системы с регулятором равен 2n, т.к. порядок объекта - n, порядок корректора динамики - (n -1), порядок корректора статики равен 1.