Занятие №9. Приведение общего уравнения кривых второго порядка к каноническому виду

№1. Привести уравнение кривой второго порядка к каноническому виду и построить кривую

Примечание: Вычислим

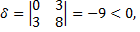
следовательно, данная кривая гиперболического типа.

Вычислим

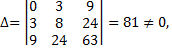
следовательно, данная кривая – гипербола.

Выполним параллельный перенос начала координат в центр кривой, который найдем из системы

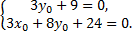
Решив систему, найдем центр кривой, точку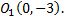

Уравнение кривой примет вид

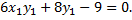
Выполнив преобразование поворота на угол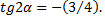

Из таблицы находим 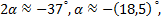тогда

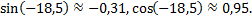
Формулы поворота примут вид

Подставив их в уравнение кривой, получим

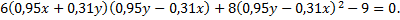
Зная, что при повороте коэффициенты при 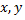обратятся в нуль, а уравнение примет вид

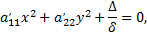
подсчитаем только коэффициенты при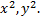

Получим

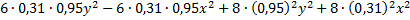
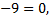
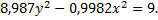
Или, учитывая то, что 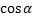и 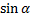вычислены приближенно, получаем 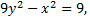т.е.

-это каноническое уравнение гиперболы.

Найдем точки пересечения кривой с осью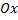

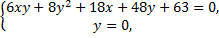
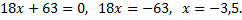
Точка пересечения с осью 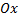заданной кривой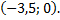

Выполним построение (рис. 77).

Рис. 77

Гипербола

№2. Привести уравнение кривой второго порядка к каноническому виду и построить кривую

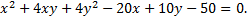
Найдем дискриминант старших членов

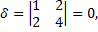
- кривая нецентральная.

Найдем дискриминант уравнения

- кривая парабола.

Выполним поворот системы координат на угол который найдем по формуле

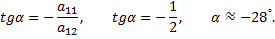
Находим 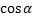и 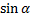по формулам

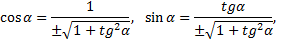
Подставим эти значения в формулы поворота

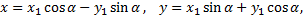
получим

Подставляем эти формулы в данное уравнение

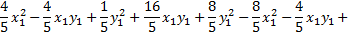
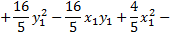
Уравнение примет вид

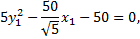
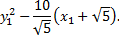
Перенесем начало координат в вершину параболы, обозначив

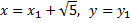
откуда 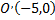-вершина параболы.

Каноническое уравнение параболы

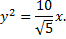
Точки пересечения параболы с осью 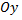найдем, решив совместно данное уравнение и уравнение оси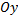

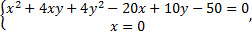
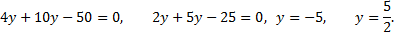
Точки пересечения кривой с осью ,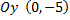

Выполним построение (рис. 78).

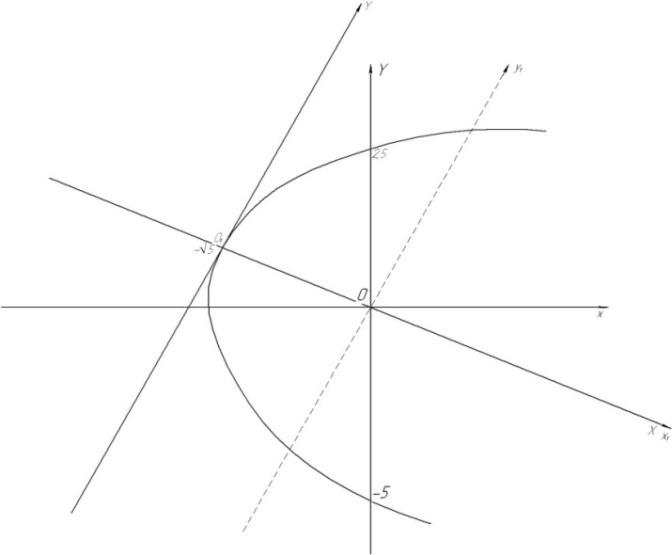
Рис. 78

Парабола