Которого являются частные производные этой функции, вычисленные в этой точке.
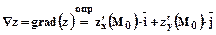 .
.
Зададим вектор 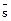 следующим образом:
следующим образом: 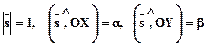 .
.
Выберем в области D произвольную 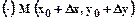 так, чтобы выполнялось условие:
так, чтобы выполнялось условие: 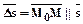 .
.
Если 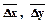 - переменные, то точка М будет перемещаться по области в данном направлении
- переменные, то точка М будет перемещаться по области в данном направлении 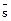 .
.




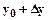 М
М
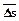


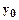 М0
М0


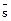
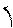
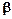
 О
О 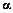
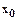
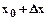
Из заданных условий следует:
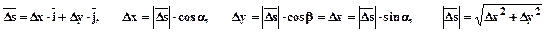 .
.
Полное приращение функции 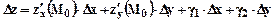 , где
, где 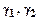 - бесконечно малые более высокого порядка малости, чем
- бесконечно малые более высокого порядка малости, чем 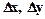 .
.
Пусть 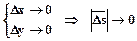 .
.
Скорость изменения функции 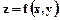 при движении точки от
при движении точки от 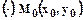 в данном направлении
в данном направлении 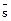 измеряется с помощью специальной производной, которую называют “производная по направлению”.
измеряется с помощью специальной производной, которую называют “производная по направлению”.
9.2. Производной по направлению данной функции 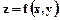 в данном направлении
в данном направлении 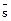 , вычисленнойв данной точке
, вычисленнойв данной точке 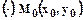 будем назывть предел отношения полного приращения функции
будем назывть предел отношения полного приращения функции 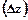 к вызвавшему его приращению вектора-направления
к вызвавшему его приращению вектора-направления 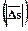 , при условии, что последнее стремится к нулю, а также при условии, что такой предел существует и конечен.
, при условии, что последнее стремится к нулю, а также при условии, что такой предел существует и конечен.
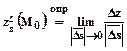 .
.
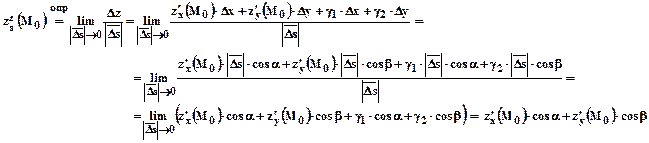
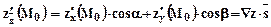 .
.
9.3. Наискорейшее возрастание функции происходит при движении от данной точки в направлении градиента.
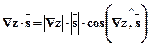 , поэтому принимает максимальное значение, когда
, поэтому принимает максимальное значение, когда 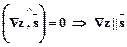 .
.
9.4. Градиент функции 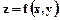 в данной
в данной 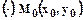 перпендикулярен к касательной линии уровня в этой точке.
перпендикулярен к касательной линии уровня в этой точке.
Линия уровня или кривая безразличия это множество всех точек в области определения функции в которых функция принимает одно и то же значение z0.
Пусть 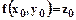 , тогда
, тогда 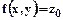 уравнение линии уровня, прохоящей через эту точку.
уравнение линии уровня, прохоящей через эту точку.
Продифференцируем последнее равенство по х, тогда получим: 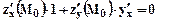 , следовательно угловой коэффициент касательной к линии уровня в
, следовательно угловой коэффициент касательной к линии уровня в 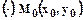 можно вычислить по формуле
можно вычислить по формуле 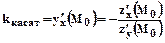 Направляющие косинусы вектора
Направляющие косинусы вектора 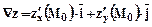 равны соответственно
равны соответственно
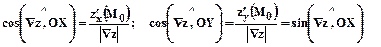 , следовательно
, следовательно 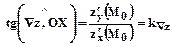 .
.
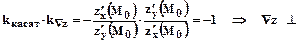 касательной.
касательной.
Дата добавления: 2015-08-26; просмотров: 954;
