Приведение плоской системы сил к данной точке

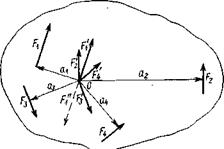Метод приведения одной силы к данной точке можно применить к какому угодно числу сил. Допустим, что в некото­рых точках тела (рис. 1.24) приложены силы F₁ F₂, F₃ и F₄. Тре­буется привести эти силы к точке О плоскости. Приведем сначала силу 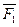приложенную в точ­ке А. Приложим (см. § 16) в точке О две силы рав­ные порознь по значению заданной силе 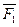параллель­ные ей и направленные в про­тивоположные стороны. В ре­зультате приведения силы 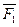получим силу 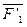, приложен­ную в точке О, и пару сил 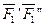с плечом 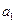. Поступив таким же образом с силой 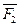, приложенной в точке В, получим силу 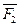, приложенную в точке О, и пару сил с плечом 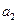и т. д. Плоскую систему сил, приложенных в точках А, В, С и D, мы заменили сходящимися силами 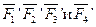, приложенными в точке О, и парами сил с моментами, равными моментам заданных сил относительно точки О:

рис.1.24

.

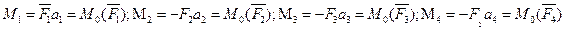Сходящиеся в точке силы можно заменить одной силой 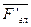равной геометрической сумме составляющих,

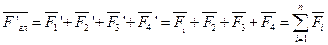
Эту силу, равную геометрической сумме заданных сил, называют главным вектором системы сил и обозначают .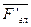

По величине проекций главного вектора на оси координат находим модуль главного вектора:

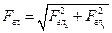
На основании правила сложения пар сил их можно заменить результирующей парой, момент которой равен алгебраической сумме моментов заданных сил относительно точки О и называется главным моментом относительно точки приведения

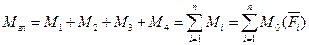
Таким образом, произвольная плоская система сил приводиться к одной силе (главному вектору системы сил) и одному моменту (главному моменту системы сил).

Необходимо усвоить, сто главный вектор 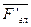не является равнодействующей данной системы сил, так как эта система не эквивалентна одной силе 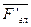. Так как главный вектор равен геометрической сумме сил заданной системе, то ни модуль, ни направление его не зависит от выбора центра приведения. Значение и знак главного момента зависит от положения центра приведения, так как плечи составляющих пар зависят от взаимного положения сил и точки (центра) относительно которой берутся моменты.

Частные случаи приведения системы сил:

1) 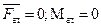; система находиться в равновесии, т.е. для равновесия плоской системы сил необходимо и достаточно, чтобы ее главный вектор и главный момент одновременно были равны нулю.

2) 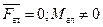тело вращается вокруг неподвижной оси ;система приводиться к паре сил, момент которой равен главному моменту.

3) 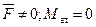тело движется прямолинейно ускоренно; система приводиться к одной равнодействующей, равной главному вектору системы.

4) 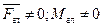- общий случай; система приводиться к главному вектору и к главному моменту.