Три способа задания движения точки. Основные кинематические параметры

Знание законов движения тела означает знание законов движения каждой его точки, поэтому изучение кинематики нач­нем с изучения движения геометрической точки.

Траекторией точкиназывается множество (геометриче­ское место) положений движущейся точки в рассматриваемой системе отсчета. В зависимости от формы траектории движение точки бывает двух видов: прямолинейное и криволинейное.

Естественный способ заключается в том, что движение точки задается ее траекторией, началом отсчета и уравнением движения по этой траектории (законом движения). В общем ви­де уравнение движения записывается следующим образом:

s=f(t)

где s — расстояние точки от начального положения, являющееся функцией времени; t — время движения точки от начального момента.

Зная траекторию точки и уравнение движения по этой тра­ектории, можно определить положение точки в любой момент времени, подставив время в равенство s=f(t).

При своем движении точка проходит некоторый путь, также являющийся функцией времени. Следует подчеркнуть, что путь, пройденный точкой, совпадает с расстоянием от начала отсчета лишь тогда, когда точка все время дви­жется в одном направлении и начало ее движения совпа­дает с началом отсчета.

Координатный способ заключаетсячается в том, что движение точки задается движением ее проекций вдоль осей координат (рис. 2.2). Уравнения плоского движения точ­ки в координатной форме записываются следующим образом: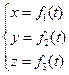

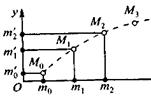рис. 2.2

Векторная величина, характеризующая в данный момент быстроту и направление движения по траектории, называется скоростью.

Скорость – вектор, в любой момент направленный по касательной к траектории в сторону направления движения. u=s\t=const (предполагается, что начала отсчета пути и времени совпадают). Единица скорости = метр в секунду = м/с.

Скорость есть величина век­торная. При прямолинейном рав­номерном движении скорость по­стоянна и по модулю, и по направ­лению, а вектор ее совпадает с траекторией (рис. 2.3, а).

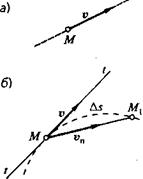При криволинейном движении скорость точки меняется по на­правлению (рис. 2.3, б). Для того чтобы установить направление вектора скорости, разобьем тра­екторию на бесконечно малые участки пути Δs, которые можно считать прямолинейными в силу их малости. Тогда на каждом участке условная скорость v_n такого прямолинейного движения будет направлена вдоль хорды. В пределе при Δs, стремящемся к нулю, хорда совпадает с касательной, следовательно, скорость в каждый момент времени направлена по касательной к тра­ектории в сторону движения (см. рис. 2.3, б).

При неравномерном движении точки модуль ее скорости ме­няется. Представим себе точку, движение которой задано естест­венным способом уравнением s=f(t). Если за небольшой промежуток времени Δt точка прошла

путь Δs, то ее средняя скорость .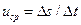

рис.2.3