Ускорение точки при криволинейном движении
При движении точки по криволинейном траектории скорость меняет свое направление. Представим себе точку М , которая за время Δt, двигаясь по криволинейной траектории, переместилась в положение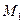 
(рис. 2.7).
Вектор приращения (изменения) скорости обозначим Δv, тогда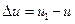 
.
Для нахождения вектора Av перенесем вектор и, в точку М и построим треугольник скоростей. Определим вектор среднего ускорения:
аср = Δv/Δt.
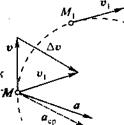Вектор аср параллелен вектору Δv, так как от деления векторной величины на скалярную направление вектора не меняется. Вектор истинного ускорения есть предел, к которому стремится отношение вектора приращения скорости к соответствующему промежутку времени, когда последний стремится к нулю: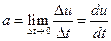 
Таким образом, истинное ускорение точки, движущейся по криволинейной траектории, равно векторной производной скорости по времени; при этом вектор ускорения всегда направлен в сторону вогнутости траектории (см. рис. 2.5). рис.2.7
Понятие о кривизне кривых линий
Ускорение точки при криволинейном движении зависит от степени изогнутости ее траектории, т. е. от кривизны траектории
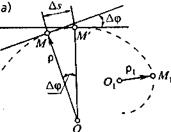
Рассмотрим криволинейную траекторию точки М (рис. 2.8, а). Угол Δφ между касательными к кривой в двух соседних точках называется углом смежности.
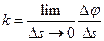
Кривизной кривой в данной точке называется предел отношения угла смежности к соответствующей длине Δs дуги, когда последняя стремится к нулю. Обозначим кривизну к, тогда:
Рассмотрим окружность радиуса R (рис. 2.8, б). Так как Δs=RΔφ, то
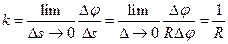рис.2.8
Следовательно, кривизна окружности во всех точках одинакова и равна к=1/R.
Для каждой точки данной кривой можно подобрать такую окружность, кривизна которой равна кривизне кривой в данной точке. Радиус р такой окружности называется радиусом кривизныкривой в данной точке, а центр этой окружности называется центром кривизны.
Итак, кривизна кривой в данной точке есть величина, обратная радиусу кривизны в этой же точке: к - 1/р.
Очевидно, что кривизна прямой линии равна нулю, а радиус кривизны равен бесконечности:
k=0, ρ=1/к =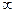 
.
Дата добавления: 2015-08-08; просмотров: 1235;