Ускорение точки

Векторная величина, характеризующая быстроту изменения скорости по величине и

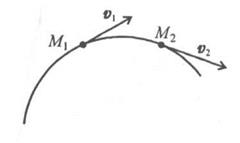
направлению, называется ускорением точки (рис.2.4).

Скорость точки при перемещении из точки М₁ в точку М₂ ме­няется по величине и направлению.

Среднее значение ускорения за этот промежуток времени:

При рассмотрении бесконечно ма­лого промежутка времени среднее ускорение превратится в ускорение в данный момент:

рис.2.4

Истинное ускорение при прямолинейном движении равно первой производной скорости или второй производной координаты по времени. Единица ускорения: метр на секунду в квадрате = м/с².

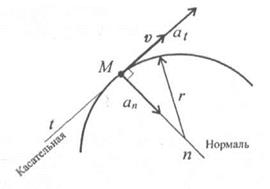Обычно для удобства рассматривают две взаимно перпендикулярно составляющие ускорения: нормальное и касательное (рис. 2.5).

Нормальное ускорение a_n характеризует изменение скорости по направлению и определяется как
,

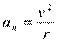где r – радиус кривизны траектории в данный момент времени.

рис.2.5

Нормальное ускорение всегда направлено перпендикулярно скорости к центру дуги.

Касательное ускорение a_t характеризует изменение скорости по величине и всегда направлено по касательной к траектории; при ускорении его направление совпадает с направлением скорости, а при замедлении оно направлено противоположно направлению вектора скорости.

рис.2.6

Формула для определения касательного ускорения имеет вид:

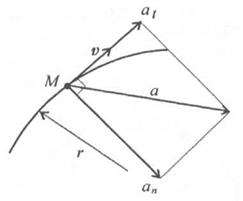
Значение полного ускорения определяется как 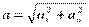(рис. 2.6).

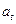* называется тангенциальным или касательным ускорением, а - номинальным или центростремительным ускорением.

Если 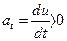, то векторы касательного ускорения и скорости направлены в одну сторону и движение ускоренное. Если 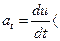0, то вектор касательного ускорения направлен в строну, противоположную вектору скорости, и движение замедленное.