Пространство и время в специальной теории относительности

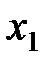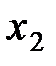Одновременность событий в разных системах отсчета. Пусть в системе К в точках с координатами и в моменты времен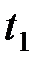и и 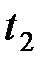происходят два события. В системе К' им соответствуют координаты 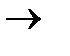и 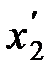и моменты времени и 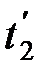. Если события в системе К происходят в одной точке 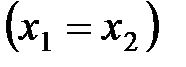и являются одновременными 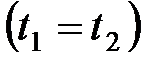, то согласно преобразованиям Лоренца (2.3), следует

, ,

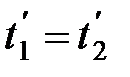т. е. эти события являются одновременными и пространственно совпадающими для любой инерциальной системы отсчета.

Если события в системе К пространственно разобщены ( 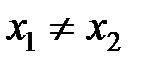), но одновременны ( ), то в системе К', согласно преобразованиям Лоренца (2.3),

.

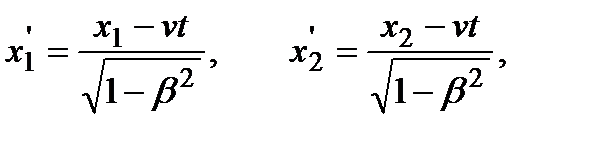
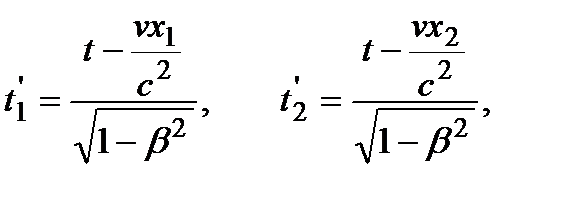
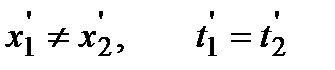Таким образом, в системе К' эти события, оставаясь пространственно разобщенными, оказываются и неодновременными. Знак разности 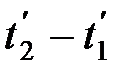определяется знаком выражения v ( 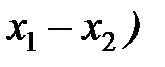, поэтому в различ­ных точках системы отсчета К' (при разных v) разность будет различной по величине и может отличаться по знаку. Следовательно, в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета, наоборот, второе событие предшествует первому.

Длительность событий в разных системах отсчета. Пусть в некоторой точке (с координатой х), покоящейся относительно системы К, происходит событие, длительность которого (разность показаний часов в конце и начале события) , где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе К'

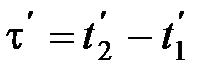(2.4)

причем началу и концу события, согласно (2.3), соответствуют

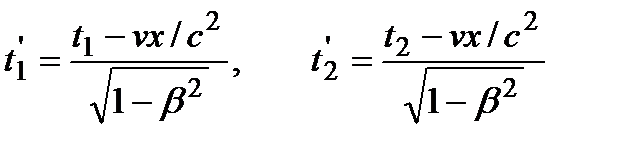. (2.5)

Подставляя (2.4) в (2.5), получим

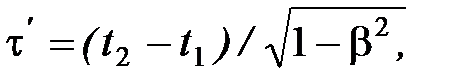(2.6)

Из соотношения (6) вытекает, что 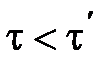, т.е. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна.

Этот результат может быть еще истолкован следующим образом: интервал времени 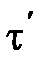, отсчитанный по часам в системе К.', с точки зрения наблюдателя в системе К, продолжительнее интервала 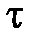, отсчитанного по его часам.

Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов, т. е. ход часов замедляется в системе отсчета, относительно которой часы движутся. В силу относительности понятий “неподвижная” и “движущаяся” системы соотношения для t и t' обратимы. Из (2.6) следует, что замедление хода часов становится заметным лишь при скоростях, близких к скорости света в вакууме.

Длина тел в разных системах отсчета.Рассмотрим стержень, расположенный вдоль оси х' и покоящийся относительно системы К'. Длина стержня в системе К.'

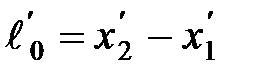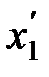, где и 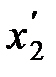— не изменяющиеся со временем t' координаты начала и конца стержня, а индекс 0 показывает, что в системе отсчета К' стержень покоится. Определим длину этого стержня в системе К, относительно которой он движется со скоростью v. Для этого необходимо измерить координаты его концов 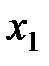и x 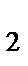в системе К в один и тот же момент времени t. Их разность 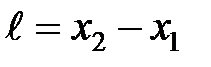и даст длину стержня в системе К. Используя преобразования Лоренца получим

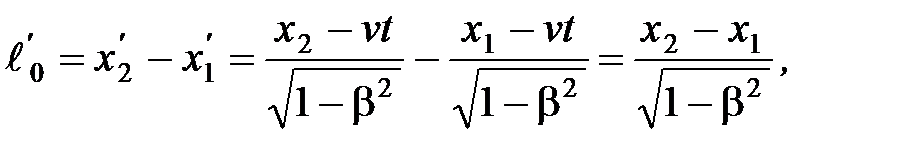
т. е. 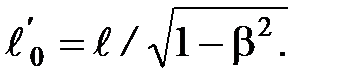(2.7)

Таким образом, длина стержня, измеренная в системе, относительно которой он движется, оказывается меньше длины, измеренной в системе, относительно которой стержень покоится. Если стержень покоится в системе К, то, определяя его длину в системе К', опять-таки придем к выражению (2.7).

Из выражения (2.7) следует, что линейный размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения в 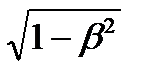раз, т. е. так называемое лоренцево сокращение длины тем больше, чем больше скорость движения. Из второго и третьего уравнений преобразований Лоренца следует, в свою очередь, что

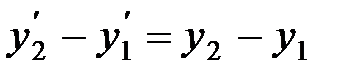и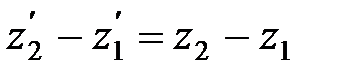

т. е. поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета. Таким образом, линейные размеры тела наибольшие в той инерциальной системе отсчета, относительно которой тело покоится.

Релятивистский закон сложения скоростей. Рассмотрим движение материальной точки в системе К', в свою очередь движущуюся относительно системы К со скоростью v. Определим скорость этой же точки в системе К. Если в системе К движение точки в каждый момент времени t определяется координатами х, у, z, а в системе К' в момент времени t' — координатами х', у', z', то

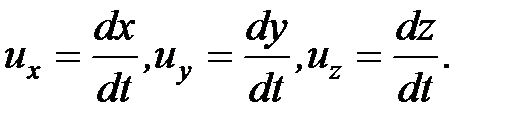
представляют собой соответственно проекции на оси х, у, z и х', у', z' вектора скорости рассматриваемой точки относительно систем К и К'.