Тема 19 Уравнение Бернулли (энергии) для элементарной струйки невязкой несжимаемой жидкости

В элементарной струйке сечениями 1-1 и 2-2 выделим некоторую массу жидкости и составим уравнение кинетической энергии (Е_к) для этой массы (рис. 41).

За время dt выделенная масса жидкости переместится и займёт положение 1¢-1¢, 2¢-2¢. Рассмотрим между сечениями три объёма: (a), (b) и (c). По условиям сплошности масса объёма (a) равна массе объёма (b).

Рисунок 41

Приращение кинетической энергии 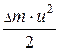при перемещении массы жидкости из положения 1-1, 2-2 в положение 1¢-1¢, 2¢-2¢:

= - .

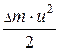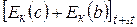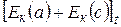При установившемся движении кинетическая энергия массы жидкости в объёме (с) в момент времени t равна кинетической энергии массы жидкости в объёме (с) в момент времени t+Dt:

=

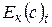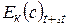
Тогда для всей выделенной массы

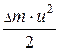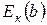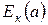= - . (19.1)

Кинетическая энергия массы жидкости в объёме (b) равна:

= ;

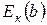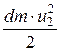dm = r × dw₂ × dl₂ = r × dw₂ × u₂ × dt;

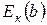= r × dw₂ × u₂ × dt × 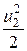. (19.2)

Аналогично, кинетическая энергия массы жидкости в объёме (а) равна:

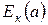= r × dw₁ × u₁ × dt × 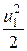. (19.3)

После подстановки (19.2) и (19.3) в выражение (19.1) получаем

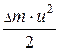= r × dw₂ × u₂ × dt × 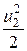- r × dw₁ × u₁ × dt × 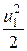. (19.4)

Для невязкой жидкости к выделенному объёму приложены силы тяжести, давления жидкости на боковую поверхность, силы давления на торцевые площадки w₁ и w₂.

Поскольку жидкость несжимаема, внутренняя энергия рассматриваемого объёма не меняется при его перемещении и в уравнение кинетической энергии входит только работа внешних сил.

При перемещении массы из положения 1-1, 2-2 в положение 1¢-1¢, 2¢-2¢ вес жидкости в объёме (с) работу не совершает и работу сил тяжести можно вычислить как работу перемещения из объёма (а) в (b).

Сила тяжести равна:

G = g × dm = g × r × dV = r × g × dw₁ × u₁ × dt.

Работа сил тяжести

G × (z₁ – z₂) = r × g × dw₁ × u₁ × dt × (z₁ – z₂). (19.5)

Работа сил давления на боковую поверхность равна нулю, так как эти силы нормальны к этой поверхности.

Работа сил давления на торцы равна разности:

р₁ × dw₁ × u₁ × dt – р₂ × dw₂ × u₂ × dt. (19.6)

Таким образом, приращение кинетической энергии (19.4) за счёт работы сил тяжести (19.5) и внешнего давления (19.6) имеет вид

r × dw₂ × u₂ × 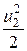× dt - r × dw₁ × u₁ × 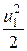× dt =

= r × g × dw₁ × u₁ × (z₁ – z₂) × dt + р₁ × dw₁ × u₁ × dt – р₂ × dw₂ × u₂ × dt.

Разделим на dt и сгруппируем

r × g × dw₁ × u₁ × z₁ + р₁ × dw₁ × u₁ + r × dw₁ × u₁ × =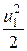

= r × g × dw₁ × u₁ × z₂ + р₂ × dw₂ × u₂ + r × dw₂ × u₂ × .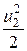

Заменим u₁ × dw₁ = dQ, u₂ × dw₂ = dQ и разделим обе части последнего уравнения на r × g × dQ.

Имеем

z₁ + 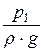+ 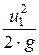= z₂ + 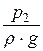+ 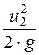. (19.7)

Это уравнение Бернулли в форме напоров для элементарной струйки между сечениями 1-1 и 2-2.

Поскольку сечения взяты произвольно, то в общем виде уравнение имеет вид:

z + 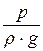+ 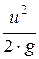= const. (19.8)

Каждое слагаемое в уравнении Бернулли в форме напоров имеет размерность длины (м) и представляет собой энергию, отнесённую к единице веса (1 Н), то есть удельнуюэнергию. Здесь z – удельнаяпотенциальнаяэнергияположения, 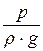– удельнаяпотенциальнаяэнергиядавления, 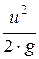– удельнаякинетическаяэнергия.

z + 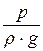+ 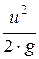= Н – полная удельная энергия в рассматриваемом сечении элементарной струйки.

Уравнение Бернулли в форме давлений имеет вид:

r × g × z + р + r × 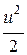= const. (19.9)

Здесь каждый член имеет размерность давления (Па) и представляет собой энергию, отнесённую к единице объёма. Здесь r × g × z – гравитационноедавление, р – статическоедавление, r × 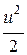– динамическоедавление.

Уравнение Бернулли имеет третью форму представления – основное уравнение Бернулли:

g × z + 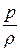+ 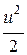= const. (19.10)

Каждое слагаемое в уравнении (19.10) характеризует энергию, отнесённую к единице массы (Дж/кг). При этом размерность каждого члена уравнения (м²/с²).