Трубка Пито-Прандтля

Рассмотрим определение местной скорости с помощью трубки Пито (рис. 43).

Эта трубка помещена в потоке жидкости изогнутым концом против течения и работает в комплексе с пьезометром. Пьезометрическаятрубкаизмеряетстатический напор 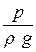, а трубкаПитоизмеряетполный напор - сумму статического и динамического 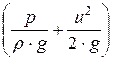. Конструктивно объединенные в одном корпусе трубка Пито и пьезометрическая трубка (кольцевое пространство с прорезями) представляет собой трубку Пито-Прандтля. Такой прибор иногда называют гидрометрической (для капельной жидкости) или пневмометрической (для воздуха) трубкой.

Рисунок 43 – Трубка Пито-Прандтля

Проведём плоскость сравнения через центр отверстия в изогнутом конце трубки Пито и напишем уравнение Бернулли для точек 1 и 2. Это уравнение записывается для элементарной струйки, так как трубка Пито в комплекте с пьезометрической трубкой измеряет местную скорость в точке, в которой она установлена:

z₁+ 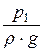+ 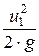= z₂ + + .

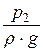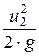В данном случае z₁ = z₂, u₁ = u, а u₂ = 0, так как при обтекании жидкостью трубки в точке 2 происходит уменьшение скорости u до нуля и в соответствии с этим увеличение давления. Тогда

+ = .

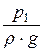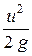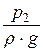Обозначим разницу показаний в трубках Пито и пьезометрической как Dh:

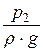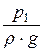- = Dh.

Уравнение Бернулли примет вид

Dh = ,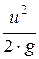

то есть трубкаПито-Прандтляизмеряетдинамическийнапор .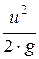

Отсюда скорость потока в данной точке равна:

u = 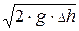. (22.1)

Если трубка Пито-Прандтля установлена на оси потока, то она измеряет максимальную скорость:

u_max = 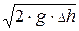. (22.2)

Чтобы трубкой Пито-Прандтля можно было непосредственно измерять скорость, к ней подключается дифференциальный манометр (в ряде случаев микроманометр).

Трубка Пито-Прандтля выполняется небольшим диаметром и с обтекаемым носком, но и в этом случае она вносит некоторое возмущение в поток. Поэтому полученное значение скорости по формулам (22.1) или (22.2) умножают на тарировочный коэффициент, определяемый опытным путём. Для заводских трубок тарировочный коэффициент равен 1…1,04.