Водомер Вентури

Расход в трубопроводе можно измерить с помощью водомера Вентури, представляющего собой вставку меньшего диаметра с плавным входом и выходом (рис.44).

Рисунок 44 – Водомер Вентури

В суженной части диаметром d₂ скорость увеличивается, а давление и пьезометрическая высота 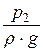= h₂ уменьшаются по сравнению с давлением и пьезометрической высотой до сужения 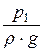= h₁. Зависимость между объёмным расходом Q и разностью h₁ - h₂ = Dh можно получить с помощью уравнения Бернулли и уравнения расхода. Расчётные сечения выберем до сужения 1-1 и в суженной части 2-2. Ввиду небольшого расстояния между сечениями и плавного сужения потери напора Dh_пот между этими сечениями будут незначительными и в первом приближении ими можно пренебречь. Если труба горизонтальна, то z₁ = z₂ и уравнение Бернулли примет вид

h₁ + a₁ × 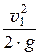= h₂ + a₂ × .

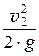С учетом того, что средняя скорость в сечении v из уравнения неразрывности течения равна отношению расхода Q к площади живого сечения потока w (v = 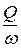) и, принимая a₁ = a₂ = 1, получим:

h₁ - h₂ = .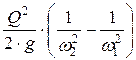

Для круглой трубы w = и тогда расход можно вычислить по формуле:

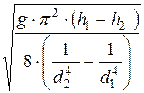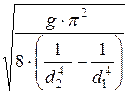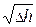Q = = × = B × ,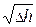

где В – постоянная величина для каждого водомера.

В = = × .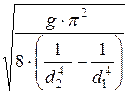

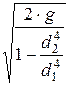Фактический расход Q_ф будет несколько меньше из-за потерь напора:

Q_ф = m × Q,

где m = тарировочный коэффициент (коэффициент расхода), значение которого меньше единицы. Обычно m = 0,95…0,97.

Тема 23 Уравнение Бернулли для сжимаемой жидкости (газа)

Для газов, обладающих вязкостью, уравнение Бернулли в дифференциальной форме (для элементарной струйки) имеет вид:

g × dz + 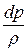+ + 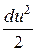g × dh = 0.

Интегрируя это уравнение вдоль элементарной струйки по длине Dl от сечения 0-0 до любого произвольного сечения, получим:

g × (z – z₀) + + 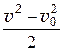g × h_пот = С, (23.1)

где h_пот – потери напора по длине Dl.

Величину можно найти, если плотность r является функцией от давления р. Вид этой функции зависит от характера термодинамического процесса, происходящего в том или другом случае движения газа. Наиболее общим случаем является политропный процесс. Из уравнения политропы 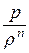= = 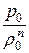const находим функцию r = f(p), которая имеет вид r =r₀ × .

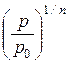После подстановки найдём

= = × = × =

= × .

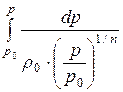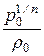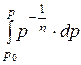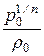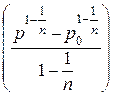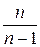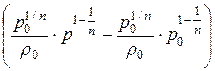Но первое слагаемое в скобках с учётом уравнения политропы 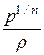= 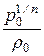равно

= = ,

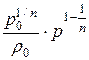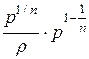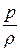а второе слагаемое

= .

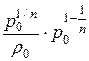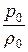Таким образом, искомая величина интеграла

= × .

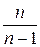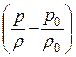Делая подстановку в уравнение (23.1), получим уравнение Бернулли в виде

g × (z – z₀) + 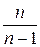× 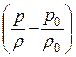+ + 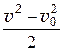g × h_пот = С.

Разделим величины и запишем уравнение Бернулли при политропном процессе для двух сечений реального газа 0-0 и любого произвольного сечения:

g × z₀ + 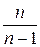× 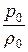+ 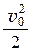= g × z + 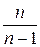× 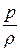+ + g × h_пот. (23.2)

Используя зависимость (1.9) 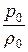= R × T₀, а 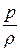= R × T, можно придать уравнению (23.2) вид

g × z₀ + 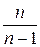×R×T₀ + 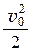= g × z + 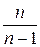×R×T + + g × h_пот. (23.3)

где R – удельная газовая постоянная.

При адиабатном процессе движение газа описывается теми же основными уравнениями, но при этом показатель политропы n заменяется показателем адиабаты k, поэтому при адиабатном процессе уравнение Бернулли будет записано в виде:

g × z₀ + 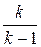× 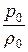+ 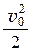= g × z + 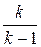× 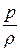+ + g × h_пот. (23.4)

или

g × z₀ + 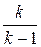×R×T₀ + 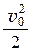= g × z + 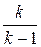×R×T + + g × h_пот. (23.5)

Рассмотрим движение газа при изотермном процессе, когда соблюдается условие

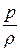= R × T = const и r = .

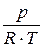В этом случае, учитывая постоянство температуры (T = const),

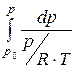= = R × T × 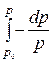= R × T × ln .

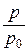Тогда для изотермного процесса уравнение Бернулли примет вид

g × z₀ + R × T₀ × ln p₀ + 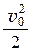= g × z + R × T × ln p + + g × h_пот. (23.6)