Тема 20 энергетический смысл и Геометрическая интерпретация уравнения Бернулли

Каждое слагаемое в уравнении Бернулли в форме напоров (19.8) имеет размерность длины (м)

z + 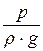+ 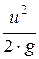= const.

Если уравнение (19.8) умножить на 1 Н, то уравнение не изменится, но размерность каждого слагаемого будет выражена в Н×м (Дж). Следовательно, каждое слагаемое в уравнении представляет собой энергию, отнесённую к единице веса (1 Н), то есть удельнуюэнергию. Тогда

z – удельная потенциальная энергия положения;

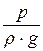– удельная потенциальная энергия давления;

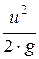– удельная кинетическая энергия.

Таким образом, 1 Н жидкости, находящийся на высоте z относительно плоскости x0y может совершать работу, равную z, Дж. Тот же 1 Н жидкости, находящийся на высоте z, обладает ещё энергией давления 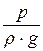, Дж. Пьезометрическая линия отделяет область изменения потенциальной энергии от области изменения кинетической энергии.

С энергетической точки зрения уравнение Бернулли можно сформулировать так:

при установившемся движении невязкой несжимаемой жидкости вдоль трубки тока сумма удельных энергий – потенциальной (положения и давления) и кинетической – есть величина постоянная.

Уравнение Бернулли показывает, что полная удельная энергия остаётся неизменной по пути данной элементарной струйки невязкой жидкости. Таким образом, уравнение Бернулли представляет собой закон сохранения механической энергии при движении идеальной жидкости.

Уравнение Бернулли в форме напоров удобно тем, что каждый член может быть представлен некоторой высотой. Так

z – геометрическая высота, то есть высота положения рассматриваемой точки пространства с жидкостью (центра тяжести сечения) над горизонтальной плоскостью сравнения x0y;

Если в уравнении Бернулли:

· р – абсолютное (полное) давление, то величина 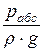= 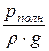– высота давления;

· р – избыточное (манометрическое) давление, то величина 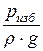= 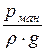называется пьезометрической высотой;

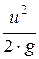– скоростная (или динамическая) высота.

Сумма 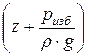= 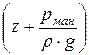характеризует пьезометрический напор.

Сумма = 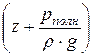характеризует гидростатический напор.

В системе координат x0y напишем уравнение Бернулли для трёх произвольных сечений элементарной струйки (рис. 42):

z₁ + 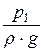+ 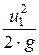= z₂ + 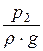+ 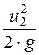=…= z_i + + ,

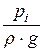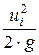или

z + 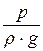+ 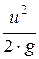= Н = const

где Н – полная высота в данном сечении струйки.

Для каждого поперечного сечения струйки величина Н может быть представлена совокупностью отрезков z, 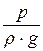и .

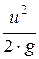Соединив между собой концы отрезков Н, получим линию, расположенную в горизонтальной плоскости. Эту плоскость и линию на ней называют плоскостью и линией полного напора.

Соединив концы отрезков 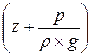, получим пьезометрическую линию.

Рисунок 42 – Геометрическая интерпретация уравнения Бернулли

Рис. 42 даёт геометрическое толкование уравнения Бернулли. Можно видеть, как по длине струйки меняются слагаемые этого уравнения. Если сечение расширяется и, следовательно, скорость уменьшается, то уменьшается скоростная высота, но возрастает сумма .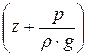

Таким образом, геометрический смысл уравнения Бернулли можно сформулировать так:

при установившемся движении невязкой несжимаемой жидкости вдоль трубки тока сумма высот – геометрической, пьезометрической и скоростной – есть величина постоянная.