Основные теоретические сведения
При движении жидкости происходит изменение положения частиц в пространстве и их деформация, то есть изменение формы и объёма.
Рассмотрим жидкую частицу, имеющую форму прямоугольного параллелепипеда с бесконечно малыми рёбрами dx, dy, dz, параллельными координатным осям (рис. 38).
Вершину А с координатами x, y, z выберем в качестве полюса. Скорость полюса в момент времени t равна u. Анализируя перемещение и деформацию выбранного объёма жидкости в пространстве, для удобства графического изображения будем рассматривать это явление в плоскости x0y, то есть на примере грани ABCD.
Частица характеризуется:
· величиной диагоналей;
· ориентацией диагоналей в пространстве;
· углами между сторонами.
Любое перемещение частицы жидкости за бесконечно малый промежуток времени можно представить в виде суммы поступательного, вращательного и деформационного движений.

Рисунок 38 – Жидкая частица
При поступательном движении частицы жидкости движутся по любой траектории (рис. 39, а). При этом не изменяются ни величины диагоналей, ни их ориентация в пространстве, ни углы между сторонами. Поступательное движение характеризуется составляющими скорости полюса u:
ux; uy; uz. (17.1)
При деформационном движении жидкой частицы изменяются углы между сторонами, величины диагоналей. Деформацию параллелепипеда можно представить как сумму объёмной (или линейной) и угловых деформаций (рис. 39, в и г).

Рисунок 39 – Поступательное движение (а), вращение (б), линейная (в) и угловая (г) деформации жидкой частицы
Линейная деформация (деформация вида растяжение- сжатие) характеризуется скоростями линейных деформаций:
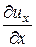 ;
; 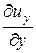 ;
; 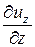 . (17.2)
. (17.2)
Угловую деформацию (или перекашивание) можно оценить изменением углов между гранями. Скорость изменения углов между гранями во времени при деформации частицы называется интенсивностью перекашивания. Скорость изменения угла перекашивания равна скорости деформации во времени. Таким образом, угловая деформация (перекашивание) характеризуется скоростями угловых деформаций:
Qx = 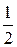 ×
× 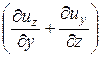 ;
;
Qy = 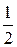 ×
× 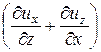 ; (17.3)
; (17.3)
Qz = 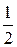 ×
× 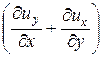 .
.
Индекс при скорости угловой деформации указывает, что угловая деформация происходит в плоскости, нормальной к данной оси координат.
При вращательном движении (рис. 39, б) не изменяются ни величина диагоналей, ни углы между сторонами, но изменяется ориентация диагоналей в пространстве. Вращательное движение жидкой частицы вокруг полюса характеризуется угловой скоростью w:
w = 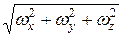 . (17.4)
. (17.4)
Угловая скорость жидкой частицы относительно мгновенной оси, проходящей через полюс, характеризуется компонентами (составляющими) угловой скорости:
wx =  ×
× 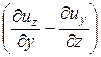 ;
;
 wy =
wy = 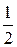 ×
× 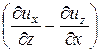 ; (17.5)
; (17.5)
wz = 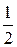 ×
× 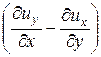 .
.
Такое представление элементарного объёма жидкости составляет содержание теоремы Гельмгольца:
скорость движения любой жидкой частицы слагается из скорости квазитвёрдого движения частицы (поступательного и вращательного движения) и скорости деформации.
Удвоенные компоненты угловой скорости wx, wy, wz называются компонентами вектора вихря W:
W = 2 × w;
Wx = 2 × wx = 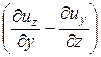 ;
;
 Wy = 2 × wy =
Wy = 2 × wy = 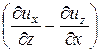 ; (17.6)
; (17.6)
Wz = 2 × wz = 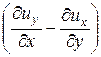 .
.
Совокупность этих векторов составляет векторное поле.
По характеру движения жидких частиц различают вихревое и потенциальное (безвихревое) движение жидкости.
Движение, при котором частицы жидкости вращаются вокруг мгновенных осей, проходящих через их полюсы, называется вихревым движением.
Движение, при котором вращение частиц вокруг мгновенных осей, проходящих через их полюсы, отсутствует, называется безвихревым (потенциальным) движением. При безвихревом движении w = 0, соответственно
wx = wy = wz = 0;
Wx = Wy = Wz = 0.
Безвихревое движение характеризуется системой:
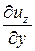 =
= 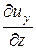 ;
;

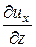 =
= 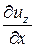 ; (17.7)
; (17.7)
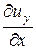 =
= 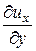
Вывод
В вершине А в момент времени t составляющие местной скорости u равны ux; uy; uz. Поступательное перемещение параллелепипеда как целого за время dt представится проекциями (рис. 39, а):
ux × dt; uy × dt; uz × dt.
Линейная деформация может быть охарактеризована удлинениями рёбер (рис. 39, в):
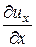 × dx × dt;
× dx × dt; 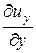 × dy × dt;
× dy × dt; 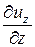 × dz × dt.
× dz × dt.
Скорости удлинения отрезков единичной длины равны соответственно
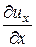 ;
; 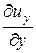 ;
; 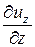 .
.
Угловая деформация характеризуется изменениями углов. Прямой угол, составленный рёбрами параллелепипеда AB и AD в плоскости x0y, при движении жидкости изменяется на сумму углов da + db (рис. 39, г).
Ввиду малости углов da и db можно принять da » tg da и db » tg db.
Угол сдвига между осью 0x и ребром AD’ найдётся так
da » tg da = 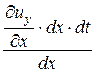 =
= 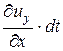 ,
,
а угол сдвига между осью 0y и стороной AB’ равен
db » tg db = 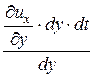 =
= 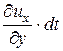 .
.
Тогда угловая деформация (деформация сдвига)
da + db = 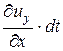 +
+ 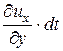 .
.
Скорость угловой деформации в плоскости x0y равна
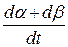 =
= 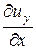 +
+ 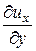 .
.
Для скоростей угловых деформаций в плоскостях y0x и x0z получим соответственно
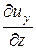 +
+ 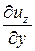 ;
; 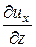 +
+ 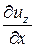 .
.
Таким образом, угловую деформацию или перекашивание можно оценить изменением углов между гранями. Скорость изменения углов между гранями во времени при деформации частицы называется интенсивностью перекашивания. Скорость изменения угла перекашивания равна скорости деформации во времени.
Qx = 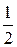 ×
× 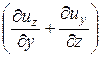 ;
;
 Qy =
Qy = 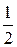 ×
× 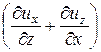 ;
;
Qz = 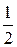 ×
× 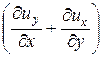 .
.
Вращение жидкой частицы можно оценить величиной и направлением угловой скорости w при повороте частицы, по изменению положения диагонали относительно координатных осей (рис. 39, б). Угловая скорость грани ABCD относительно оси 0z найдётся как
wz = 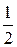 ×
× 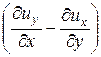 .
.
Для угловых скоростей граней относительно осей 0x и 0y получим выражения
wx = 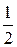 ×
× 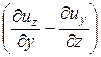 ;
;
wy = 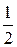 ×
× 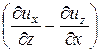 .
.
Дата добавления: 2015-08-26; просмотров: 1245;
