Тема 14 Способы описания движения жидкости
Жидкость представляет собой совокупность частиц, заполняющих объём без пустот и разрывов.
Жидкая частица – часть жидкости, малая по сравнению с объёмом рассматриваемой жидкости, и в то же время объём частицы велик по сравнению с объёмом молекулы жидкости. В частице содержится так много молекул, что жидкость в пределах частицы можно считать сплошной средой – континуумом.
Предположение о сплошности позволяет считать все параметры, характеризующие движущуюся жидкость, непрерывными в пространстве и времени и дифференцируемыми.
В процессе движения жидкости изменяются во времени взаимные положения жидких частиц и их форма. Положение жидкой частицы определяется координатами некоторой точки, выбранной произвольно в пределах частицы. Эта точка называется полюсом. Под скоростью частицы понимается скорость выбранного полюса. В общем случае движение частицы можно считать определённым, если известны законы движения всех частиц, то есть положение каждой частицы задано как функция времени.
Существуют два способа описания движений жидкости.
1. Способ Лагранжа. В этом способе предлагается рассматривать движение каждой частицы жидкости. В начальный момент времени положение частицы определено начальными координатами её полюса x0, y0, z0. При движении частица перемещается, и координаты её полюса изменяются. Движение частицы определено, если для каждой частицы можно указать координаты x, y, z как функции начального положения (x0, y0, z0) и времени t:
x = x (x0, y0, z0, t);
y = y (x0, y0, z0, t); (14.1)
z = z (x0, y0, z0, t).
Переменные x0, y0, z0 и t называют переменными Лагранжа. Совокупность приведенных функций (13.1) описывает траектории движений частиц жидкости. Из уравнений (13.1) можно найти проекции на координатные оси скоростей и ускорений всех жидких частиц. Если обозначить через u вектор скорости жидкой частицы, то проекции скоростей
ux = 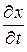 ; uy =
; uy = 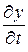 ; uz =
; uz = 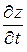 (14.2)
(14.2)
и ускорений
ax = 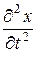 ; ay =
; ay = 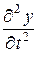 ; az =
; az = 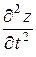 . (14.3)
. (14.3)
При описании движений жидкости методом Лагранжа можно пользоваться также криволинейными координатами.
Способ Лагранжа находит применение при решении ряда специальных задач, например волновых движений.
2. Способ Эйлера. В этом способе фиксируют не частицы жидкости, а точки пространства, через которые проходят в разные моменты различные частицы жидкости. В этих точках пространства определяют значения скорости движения сплошной среды. По методу Эйлера задача заключается в изучении поля скоростей, ускорений и других параметров в фиксированных точках пространства:
u = f (x, y, z, t);
j = f (x, y, z, t); (14.4)
p = f (x, y, z, t).
где u, j, p – мгновенная местная скорость, ускорение и давление соответственно;
x, y, z, t – переменные Эйлера (координаты x, y, z и время t).
Тема 15 Основные понятия движения жидкости и газа
Мгновенная местная скорость u – скорость частицы жидкости в данный момент времени в каждой точке в пределах движущегося потока.
Векторное поле скоростей – совокупность мгновенных местных скоростей.
Векторными линиями поля скоростей являются линии тока. Линия тока – кривая, в каждой точке которой в данный момент времени вектор местной скорости направлен по касательной. Важной особенностью совокупности линий тока в фиксированный момент времени является то, что они не пересекаются друг с другом.
Траектория движения частицы жидкости – геометрическое место последовательных положений элементарной частицы жидкости при её движении в пространстве. Другими словами – это след движения отдельной частицы жидкости в пространстве. При установившемся движении линии тока и траектории движения жидкой частицы совпадают.
Совокупность линий тока, проведенных через все точки бесконечно малого замкнутого контура, образует поверхность, называемую трубкой тока. Поверхность трубки тока является непроницаемой, то есть жидкость не может ни вытекать из неё, ни поступать в неё.
Элементарная струйка жидкости – масса жидкости внутри трубки тока. При неустановившемся движении форма трубки тока непостоянна. При установившемся движении трубка тока и элементарная струйка остаются неизменными.
Свойства элементарной струйки
1. Длина её неограниченна, а сечение очень мало.
2. Вследствие малости поперечного сечения элементарной струйки скорости во всех точках её поперечного сечения являются одинаковыми.
3. Поверхность является непроницаемой для частиц жидкости, движущихся в соседних струйках.
Совокупность элементарных струек, движущихся с разными скоростями и скользящими одна по другой, называется потоком жидкости.
По характеру изменения поля скоростей во времени движение жидкости делится на установившееся и неустановившееся.
Неустановившееся (нестационарное) движение такое, при котором в точках области, где движется жидкость, местные скорости изменяются с течением времени. При неустановившемся движении все элементы движения (скорость u, ускорение j, давление р, плотность r, глубина h) являются функцией и координат (x, y, z) и времени t:
u = f(x, y, z, t);
j = f(x, y, z, t); (15.1)
p = f(x, y, z, t).
Установившееся (стационарное) движение такое, при котором поле скоростей не меняется с течением времени. В любой точке потока жидкости скорость, давление и ускорение остаются постоянными, то есть не изменяются во времени ни по величине, ни по направлению и являются функцией только координат:
u = f(x, y, z);
j = f(x, y, z); (15.2)
p = f(x, y, z).
Примером неустановившегося движения может быть течение в поршневых насосах и компрессорах, процессы наполнения или опорожнения резервуаров газохранилищ, обтекание здания при порывистом ветре.
Примером установившегося движения является истечение жидкости из резервуара при поточном расходе, обтекание потоком воздуха зданий при постоянной скорости ветра.
Установившееся движение может быть равномерным и неравномерным.
Равномерным называется такое установившееся движение, при котором живые сечения потока и средняя скорость v в них одинаковы по его длине, а скорости в соответствующих точках всех живых сечений также одинаковы. При равномерном движении линии тока представляют собой систему прямых параллельных линий, поэтому такое движение называют также параллельно-струйным или продольно однородным.
Неравномерным называется такое установившееся движение жидкости, при котором живые сечения и средние скорости потока изменяются по его длине, скорости в соответствующих точках живых сечений не одинаковы.
Иллюстрацией равномерного движения является движение жидкости в трубе постоянного диаметра при постоянном давлении.
При неравномерном движении, когда линии тока непараллельны и (или) криволинейны различают:
· резкоизменяющееся движение;
· плавноизменяющееся движение, при котором можно пренебречь кривизной линий тока и их непараллельностью (угол расхождения между отдельными линиями тока очень мал). При этом с достаточной для практических целей точностью можно построить плоское живое сечение. Давление распределяется по живому сечению по гидростатическому закону, то есть по закону прямой линии.
Движение жидкости можно рассматривать в одномерном приближении, когда продольные размеры потока во много раз превосходят его поперечные размеры. Это имеет место главным образом в трубах, реках и каналах. При этом на неподвижных границах скорость жидкости равна нулю.
В гидрогазодинамике потоки разделяют на напорные, безнапорные и струйные. Если поток со всех сторон ограничен твёрдыми стенками, то он называется напорным. Если только часть потока ограничена твёрдыми стенками, а на остальной части жидкость граничит с газом, в частности с атмосферой (поток имеет свободную поверхность), то такое движение называется безнапорным. Если поток не ограничен твёрдой поверхностью, то он называется струйным (или струёй). Струя жидкости может быть ограничена той же самой жидкостью (затопленная струя) или газом (свободная струя).
Объёмным расходом потока Q называется объём жидкости V, проходящий в единицу времени t через живое сечение потока, м3/с:
Q = 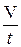 . (15.3)
. (15.3)
Массовым расходом потока Qm называется масса жидкости m, проходящий в единицу времени t через живое сечение потока, кг/с:
Qm = 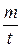 . (15.4)
. (15.4)
Живым сечением потока w называют поперечное сечение потока, перпендикулярное его направлению.
Смоченный периметр c (хи) – часть периметра живого сечения, на которой жидкость соприкасается с твёрдыми стенками.
Гидравлическим радиусом R называют отношение площади живого сечения потока w к смоченному периметру c:
R = 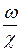 . (15.5)
. (15.5)
В случае напорного течения в круглой трубе R = 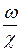 =
= 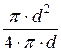 =
= 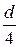 , то есть гидравлический радиус вдвое меньше геометрического.
, то есть гидравлический радиус вдвое меньше геометрического.
Диаметр эквивалентный dэкв – отношение четырёх площадей живого сечения потока w к смоченному периметру c:
dэкв = 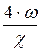 = 4 × R. (15.6)
= 4 × R. (15.6)
В случае напорного течения в круглой трубе dэкв = 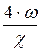 =
= 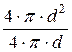 = d.
= d.
Средней скоростью потока v в данном сечении называют отношение объёмного расхода потока Q к площади его живого сечения w, м/с:
v = 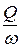 . (15.7)
. (15.7)
Следовательно, средняя скорость, это та скорость, которую должны были бы иметь все частицы потока, чтобы через данное живое сечение прошёл расход Q, соответствующий действительным скоростям этих частиц.
Если речь идёт о массовом расходе, то средняя скорость определяется из выражения:
v = 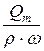 . (15.8)
. (15.8)
Тема 16 Уравнения полей скоростей и ускорений (уравнения кинематики Эйлера)
Движение жидкости характеризуется, в основном, параметрами движения – скоростью и ускорением.
При неустановившемся движении поле скоростей изменяется во времени, то есть для одной и той же точки пространства скорость движения жидкости различна в различные моменты времени.
Обозначим через ux, uy, uz проекции скоростей на оси координат. Тогда неустановившеесядвижение потока жидкости описывается системой уравнений:
ux = f1 (x, y, z, t);

uy = f2 (x, y, z, t); (16.1)
uz = f3 (x, y, z, t).
Величина полной скорости равняется:
u = 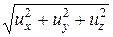 . (16.2)
. (16.2)
Для установившегосядвижения система уравнений будет иметь вид:
ux = f1 (x, y, z);

uy = f2 (x, y, z); (16.3)
uz = f3 (x, y, z).
Располагая уравнениями (16.1) и (16.2), можно определить скорость в данной точке по величине и направлению, а также ускорение j. Величина ускорения j определяется выражением:
j = 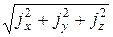 , (16.4)
, (16.4)
где проекции ускорения соответственно равны:
jx = 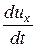 ; jy =
; jy = 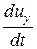 ; jz =
; jz = 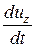 .
.
В общем случае неустановившегося движения проекции скорости ux, uy, uz являются функциями переменных Эйлера (координат x, y, z и времени t). Поэтому полный дифференциал скорости равен сумме четырёх частных дифференциалов:
dux = 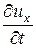 × dt +
× dt + 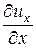 × dx +
× dx + 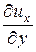 × dy +
× dy + 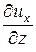 × dz,
× dz,
а её производная по времени
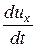 =
= 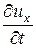 +
+ 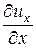 ×
× 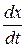 +
+ 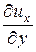 ×
× 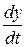 +
+ 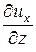 ×
× 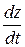 . (16.5)
. (16.5)
Рассматривая dx, dy, dz как проекции элементарного перемещения dl на оси координат, получим:
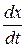 = ux;
= ux; 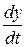 = uy;
= uy; 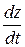 = uz.
= uz.
Тогда уравнение (16.5) запишется в виде
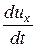 =
= 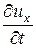 +
+ 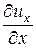 × ux +
× ux + 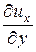 × uy +
× uy + 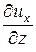 × uz.
× uz.
Аналогичные выражения можно составить также для производных 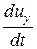 и
и 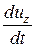 , в результате чего получим выражения для проекций ускорения в координатах Эйлера.
, в результате чего получим выражения для проекций ускорения в координатах Эйлера.
jx = 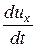 =
= 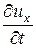 +
+ 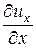 × ux +
× ux + 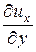 × uy +
× uy + 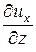 × uz.
× uz.
 jy =
jy = 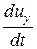 =
= 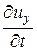 +
+ 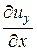 × ux +
× ux + 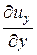 × uy +
× uy + 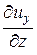 × uz. (16.6)
× uz. (16.6)
jz = 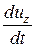 =
= 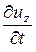 +
+ 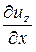 × ux +
× ux + 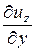 × uy +
× uy + 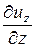 × uz.
× uz.
Полученная система получила название уравнения кинематики Эйлера или уравнения неустановившегося движения жидкости.
Уравнение потока (16.6) слагается из локальной 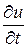 и конвективной
и конвективной 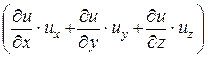 составляющих. Локальная составляющая представляет собой интенсивность изменения скорости в данной фиксированной точке пространства (при неизменных координатах x, y, z). Она обусловлена неустановившемся характером движения жидкости. Конвективная составляющая характеризует изменение скорости частицы при её перемещении относительно координатных осей – ускорение при перемещении частицы в пространстве.
составляющих. Локальная составляющая представляет собой интенсивность изменения скорости в данной фиксированной точке пространства (при неизменных координатах x, y, z). Она обусловлена неустановившемся характером движения жидкости. Конвективная составляющая характеризует изменение скорости частицы при её перемещении относительно координатных осей – ускорение при перемещении частицы в пространстве.
При установившемся движении локальная производная равна нулю
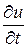 = 0.
= 0.
В случае установившегося движения уравнения имеют вид:
jx = 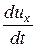 =
= 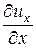 × ux +
× ux + 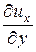 × uy +
× uy + 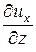 × uz.
× uz.
 jy =
jy = 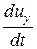 =
= 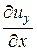 × ux +
× ux + 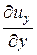 × uy +
× uy + 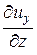 × uz. (16.7)
× uz. (16.7)
jz = 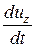 =
= 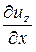 × ux +
× ux + 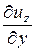 × uy +
× uy + 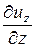 × uz.
× uz.
Дата добавления: 2015-08-26; просмотров: 4612;
