Распределение давления при политропном процессе

В этом случае из уравнения политропы (12.3) r = r₀ × 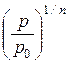. Делая подстановку в основное дифференциальное уравнение гидростатики(12.4), получим

dp = – r × g × dz = – r₀ × 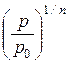× g × dz,

откуда

dz = – × .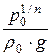

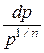Интегрируя, получим

(z₂ – z₁) = × = × × =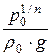

= × .

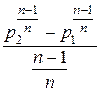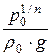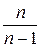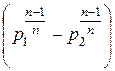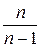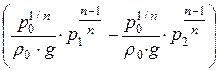Из уравнения политропы (12.3) можно записать

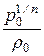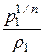= и = .

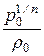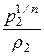С учётом этой записи предыдущее выражение принимает вид

(z₂ – z₁) = × = × .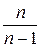

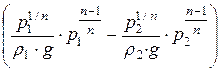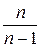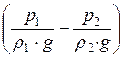Мы получили уравнение, которое определяет закон распределения давления при политропном процессе:

g × z₁ + 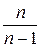× 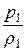= g × z₂ + 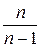× 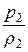(12.9, а)

или в более общей форме

g × z + 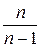× 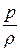= g × z + 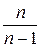× 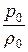(12.9, б)

Для адиабатного процесса, заменяя показатель политропы n на показатель адиабаты k, имеем

g × z + 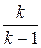× 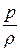= g × z + 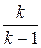× 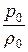(12.10)