Тема 12 Равновесие газов

Газы относятся к сжимаемым жидкостям и уравнения равновесия должны учитывать их сжимаемость. Поэтому дифференциальные уравнения равновесия для газов должны быть дополнены характеристическими уравнениями, связывающими плотность r, давление p и температуру T.

Итак, для газов справедливы:

· дифференциальное уравнение равновесия (4.6)

dp = r × (X × dx + Y × dy + Z × dz);

· уравнение поверхности уровня (5.1)

X × dx + Y × dy + Z × dz = 0;

· характеристическое уравнение r = f(p, T).

Связь между плотностью, давлением и температурой устанавливает уравнение состояния газа (1.9):

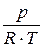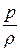r = или = R × T или pV_уд = R × T,

где р - абсолютное давление, Па;

Т - абсолютная температура, К. Т = (273 + );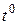

V_уд – удельный объём;

R - удельная газовая постоянная, различная для разных газов, но не зависящая от температуры и давления, Дж/(кг К);

r - плотность, кг/м³.

В случае изотермного процесса изменение давления и объёма газа происходит при поддержании одной и той же температуры (Т = const). Уравнение состояния определяется законом Бойля-Мариотта:

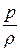= const или pV_уд = const. (12.1)

Адиабатный процесс представляет собой случай изменения давления в условиях отсутствия теплообмена. Уравнение адиабаты имеет вид:

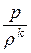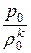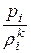= = … = = const, (12.2)

где k – показатель адиабаты.

Общим случаем является политропный процесс. Уравнение политропы записывается в виде:

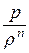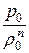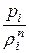= = … = = const, (12.3)

где n – показатель политропы.

В связи с указанными вариантами характеристического уравнения рассмотрим закон распределения давления в следующих трёх предположениях:

а) плотность постоянна (r= const) при небольшой высоте столба газа;

б) плотность изменяется, подчиняясь изотермному закону (Т = const);

в) плотность изменяется по уравнению политропы (12.3).

Расположим координатную систему так, чтобы оси 0x и 0y были горизонтальны, а ось 0z была направлена вертикально вверх. Тогда для жидкости в поле земного тяготения проекции ускорения массовой силы (силы тяжести) на координатные оси равны:

X = g_x = 0; Y = g_y = 0; Z = g_z = – g,

где g_x, g_y и g_z – проекции ускорения g по координатным осям.

Тогда из основного дифференциального уравнения гидростатики (4.6) имеем:

dp = – r × g × dz (12.4)

12.1 Распределение давления при небольшой высоте столба газа (r = const)

Запишем уравнение (12.4) в виде 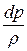+ g × dz = 0 и проинтегрируем с учётом r = const. Подучим:

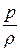+ g × z = С, (12.5)

Постоянная интегрирования С определяется из условий на границе. Если на некоторой заданной высоте z₀ известно давление р₀, то подставляя эти значения в уравнение (12.5) найдём

С = 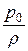+ g × z₀.

Следовательно,

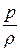+ g × z = 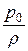+ g × z₀

или

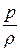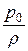= + g × (z₀ - z). (12.6)

Из этого уравнения видно, что давление убывает с увеличением высоты расположения данной точки.

Таким образом, при небольшой высоте столба газа и постоянной плотности r распределение давления аналогично таковому для капельной жидкости (уравнение 6.3).