Вывод уравнения. Расположим координатные оси 0x и 0y в плоскости свободной поверхности жидкости и направим ось 0z вертикально вверх

Расположим координатные оси 0x и 0y в плоскости свободной поверхности жидкости и направим ось 0z вертикально вверх. Допустим, что внутри жидкости расположена невесомая, жёсткая, непроницаемая криволинейная пластинка, не имеющая толщины. Такая пластинка будет неподвижной. Требуется определить, с какой силой жидкость давит на эту пластинку (рис. 24, а).

Силы давления на верхнюю сторону пластинки F’ и на нижнюю F равны между собой, но направлены в прямо противоположные стороны и взаимно уравновешены. Найдём одну из них, например F, равнодействующую элементарных сил dF.

Так как поверхность пластинки криволинейна, то силы dF образуют систему непараллельных сил. Такая система в общем случае приводится к главному вектору и одной паре сил.

Разложим каждую элементарную силу dF на три составляющие по координатным осям, то есть dF_x, dF_y и dF_z:

dF_x = p × cosa × dw;

dF_y = p × cosb × dw; (а)

dF_z = p × cosg × dw,

где a, b, g – углы наклона элементарных сил dF к координатным осям, различные для разных площадок dw.

Суммируя проекции элементарных сил, найдём соответствующие проекции равнодействующей силы F:

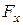= å p × cosa × dw;

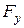= å p × cosb × dw;

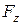= å p × cosg × dw.

Сила F по величине будет равна:

F = 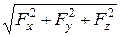. (9.1)

Направление линии действия силы F определяется по направляющим косинусам:

cosa = 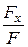; cosb = 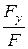; cosg = 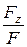. (9.2)

Указанный способ решения осложняется или даже становится невозможным, если поверхность w не может быть выражена алгебраически в виде функции w(x, y, z). Для упрощения решения систему уравнений (а) запишем в виде:

dF_x = p × dw × cosa = p × dw_x;

dF_y = p × dw × cosb = p × dw_y;

dF_z = p × dw × cosg = p × dw_z,

где р – гидростатическое давление в точке;

dw_x – проекция площадки dw на вертикальную плоскость, перпендикулярную оси 0x (на плоскость y0z);

dw_y и dw_z – проекции площадки dw на плоскости, перпендикулярные осям 0y и 0z.

Выражение (p∙dw_x) представляет собой силу давления жидкости на элементарную площадку dw_x (рис. 24, б).

Интегрируя, получим

F_x = = .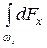

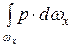Но интеграл 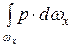представляет собой силу давления жидкости на всю плоскую площадку w_x, поэтому

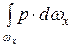= r × g × h_сx × w_x,

Итак, получаем формулу (9.3):

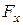= r × g × h_сx ×w_x,

где w_x – проекция криволинейной поверхности w на плоскость, перпендикулярную оси 0x;

h_сx – глубина погружения центра тяжести площади w_x под уровень свободной поверхности.

По аналогии получаем формулу (9.4):

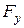= r × g × h_сy × w_y,

где w_y – проекция криволинейной поверхности w на плоскость, перпендикулярную оси 0y;

h_сy – глубина погружения центра тяжести проекции w_y под уровень свободной поверхности.

Вертикальная проекция силы F, то есть сила F_z равна:

F_z = = ,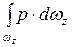

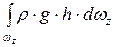где h – глубина погружения площадки dw под уровень свободной поверхности.

Произведение h × dw_z можно рассматривать как элементарный объём dV. Поэтому силу F_z можно выразить как (рис. 24, в):

F_z = 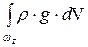= r × g × 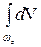= r × g × V.

Это формула (9.5)

F_z = r × g × V.

где V – объём тела давления.