Вывод уравнения

Определим силу гидростатического давления на площадь w, лежащую в плоскости стенки, расположенной под углом Q к горизонту (рис. 22).

За ось координат 0z примем линию, совпадающую с проекцией площадки на плоскость рисунка, и продолжим её до пересечения с уровнем свободной поверхности жидкости в точке 0. Из точки 0 проведём ось 0x , нормальную к плоскости рисунка. Дополнительно, для большей наглядности повернём плоскость стенки вместе с выбранной на ней площадкой w вокруг оси 0z до совмещения с плоскостью рисунка (то есть на 90°). Тогда координатная ось 0x займёт положение 0x’, ось 0z останется на месте, а площадка w изобразится на рисунке в натуральную величину.

В каждой точке выбранной площадки w гидростатическое давление равно:

р = ,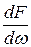

где dF – элементарная сила;

dw – элементарная площадка.

Отсюда dF = р × dw. Следовательно, сила действующая на всю стенку равна:

F = 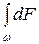= 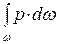. (а)

В любой точке площадки на основании основного уравнения гидростатики полное (абсолютное) давление р равно:

р = р_св + r × g × h. (б)

Тогда

F = 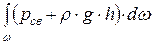. (в)

Здесь

h = l × sinQ, (г)

где l – расстояние от свободной поверхности, считая по наклону стенки, до данной точки.

Следовательно,

F = =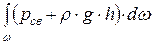

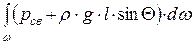
или

F = p_св × w + r × g × sinQ × 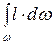. (д)

Подынтегральная функция l × dw – это статический момент площадки dw относительно оси 0x’. Тогда интеграл – это сумма статических моментов всех элементов площади w , то есть статический момент самой площади w.

Статический момент площади относительно любой оси, лежащей в той же плоскости, равен произведению этой площади на расстояние от центра тяжести до оси моментов. Тогда

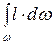= l_С × w.

где l_С – расстояние от свободной поверхности, считая по наклону стенки, до центра тяжести С смоченной поверхности (площади).

После подстановки в (д) получим

F = p_св × w + r × g × l_С × sinQ ×w.

С учётом выражения (г) получаем формулу (8.1)

F = p_св × w + r × g × h_с × w.