Основные теоретические сведения. Равнодействующая сил давления на плоскую стенку w (рис

Равнодействующая сил давления на плоскую стенку w (рис. 22) определяется по формуле:

F = p_св × w + r × g × h_с × w, (8.1)

где w - площадь смоченной поверхности плоской стенки, м²:

h_с - глубина погружения центра тяжести С смоченной площади под уровень свободной поверхности, м;

p_св – внешнее давление (на свободную поверхность жидкости);

Произведение h_с × w - это объём цилиндра с площадью основания w и высотой h_с.

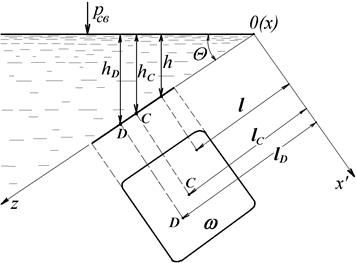
Рисунок 22 – К определению силы давления на плоскую стенку

В уравнении (8.1):

p_св × w = F_вн- сила внешнего давления, передаваемая на стенку по закону Паскаля, Н;

r × g × h_с × w = F_ж - сила давления самой жидкости на стенку, Н.

Следовательно, сила, с которой жидкость давит на плоскую стенку, равна весу жидкости в объёме цилиндра с основанием, равным площади данной стенки, и высотой, равной глубине погружения центра тяжести этой площади под уровень свободной поверхности:

F_ж = r × g × h_с × w. (8.2)

Так как r × g × h_с = р_с, где р_с – гидростатическое давление в центре тяжести площадки w, можно записать:

F_ж = р_с × w.

Точка приложения равнодействующей сил давления на наклонную стенку лежит ниже центра тяжести – в центре давления D.

Глубина погружения центра давления под уровень свободной h_D поверхности жидкости равна:

h_D = l_D × sinQ, (8.3)

l_D – расстояние от свободной поверхности до центра давления D, считая по наклону стенки4

Q – угол наклона стенки к горизонту.

Расстояние от свободной поверхности до центра давления D, считая по наклону стенки l_D, определяется по формуле:

l_D = l_С + 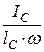, (8.4)

где l_С – расстояние от свободной поверхности до центра тяжести С, считая по наклону стенки;

I_C – момент инерции смоченной площади относительно оси, проходящей через центр тяжести С параллельно линии уреза жидкости.

Совпадать глубина погружения центра тяжести смоченной поверхности С и центра давления D может только в случае, если площадка горизонтальная или она лежит на бесконечно большой глубине.