Уравнение Бернулли для элементарной струйки невязкой сжимаемой жидкости

Плотность сжимаемой жидкости изменяется в процессе движения. Проинтегрировав дифференциальное уравнение одномерного движения жидкости для струйки, получаем:

.

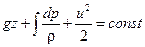(2.56)

При установившемся движении влияние сжимаемости практически проявляется только в газах, при анализе течения которых удельной энергией положения можно пренебречь. Тогда:

.

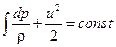(2.57)

Это уравнение можно назвать уравнением Бернулли для сжимаемой жидкости. Член 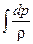характеризует потенциальную энергию газа с учетом преобразования его внутренней энергии.

Вывод: При установившемся течении невязкого газа сумма удельной потенциальной, внутренней и кинетической энергии есть величина постоянная.

Для вычисления интеграла 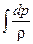необходимо знать процесс изменения состояния газа при этом течении. Если считать что течение происходит без теплообмена, то для невязкого газа это будет отвечать изоэнтропическому изменению состояния. Такой процесс описывается уравнением

,

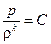(2.58)

где k – показатель адиабаты процесса; С – постоянная.

Подставим в интеграл 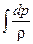вместо ρ его значение из предыдущего уравнения 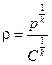, тогда .

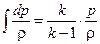Теперь уравнение Бернулли для сжимаемой жидкости принимает вид

.

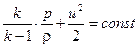Поскольку отношение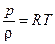

.

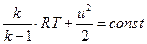(2.59)

Из этого уравнения следует, что изменение скорости вдоль трубки тока сжимаемого газа связано с изменением температуры. При увеличении скорости температура падает и наоборот.