Уравнение Бернулли для потока вязкой сжимаемой жидкости
При составлении уравнений движения сжимаемой жидкости следует учитывать, что не только скорости, но и плотности, температуры и давления отдельных струек в пределах живых сечений неодинаковы, что значительно усложняет исследование. Поэтому поток конечных размеров рассматривают как одну струйку. Заменив в уравнении для струйки скорость струйки u на среднюю скорость потока uср, можно сразу написать уравнение Бернулли сжимаемой невязкой жидкости:
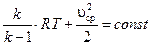 . .
| (2.60) |
Теперь составим уравнение Бернулли для вязкой сжимаемой жидкости, для чего запишем дифференциальное уравнение движения
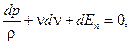
интегрирование которого для сжимаемой жидкости зависит от конкретных условий движения и закона изменения состояния газа.
При адиабатическом течении, где отсутствует обмен тепла со средой вне границ потока, можно получить уравнение движения в конечном виде, для чего необходимо применить понятие энтальпии
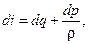
| (2.61) |
где q – количество тепла, передаваемое 1 кг газа.
Подставив уравнение энтальпии в уравнение Бернулли, получим
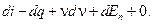
При адиабатическом течении энергия, потерянная на трение, переходит во внутреннее тепло (dEn = dq), тогда
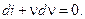
Проинтегрировав, получим
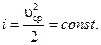
| (2.62) |
Мы получили основное уравнение адиабатического течения газа.
Вывод: Сумма удельной кинетической энергии и энтальпии остается неизменной в процессе движения газа.
Можно доказать, что для воздуха сжимаемостью можно пренебречь, если скорость течения не превышает 70 м/с, для природного газа – 90 м/с. В системах вентиляции и газопроводов низкого давления скорости течения не превышают указанных пределов, поэтому расчет в этих системах ведется как для несжимаемой жидкости. В этих системах расчет можно вести по уравнению Бернулли в форме давлений
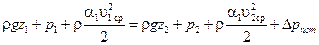 .
.
Дата добавления: 2015-08-26; просмотров: 1112;
