Дифференциальное уравнение движения невязкой жидкости (уравнение Эйлера)
Предположим, что в жидкости движется элементарный объем в форме параллелепипеда со сторонами dx, dy, dz (см. рис. 2.38). На параллелепипед действуют поверхностные силы давления и массовые силы с проекциями X, Y, Z, отнесенными к единице массы. При движении объема возникают силы инерции. Проекции этих сил на оси координат, отнесенные к единице массы, равны соответственно: 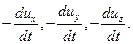

Рис. 2.38. Схема равномерного движения объема жидкости
Рассмотрим условие равновесия сил, в проекции на ось х. Сила давления на левую грань – pdydz, на правую грань
–(p + 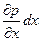 )dydz,
)dydz,
где 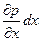 =Δp – изменение давления вдоль оси x.
=Δp – изменение давления вдоль оси x.
Массовая сила равна Xρdxdydz. Уравнение равновесия запишется в виде
pdydz – (p + 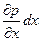 ) dydz + Xρdxdydz
) dydz + Xρdxdydz 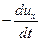 ρdxdydz = 0,
ρdxdydz = 0,
или
– 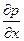 dxdydz + Xρdxdydz
dxdydz + Xρdxdydz 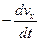 ρdxdydz = 0.
ρdxdydz = 0.
Разделив каждый член уравнения на ρdxdydz, получим
X – 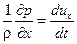 .
.
Соответственно для осей и уравнение равновесия будет выглядеть следующим образом
Y – 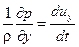 ,
,
Z – 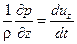 .
.
Объединив полученные уравнения, получим систему уравнений Эйлера:
X – 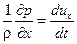 ,
,
Y – 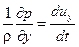 , ,
| (2.42) |
Z – 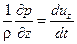 .
.
Можно получить полный дифференциал уравнений Эйлера для установившегося движения, если рассматривать перемещение частиц жидкости вдоль линии тока. Для этого надо умножить каждое из уравнений системы на соответствующую проекцию элементарного перемещения частиц dx, dy, dz, и сложить их:
(Xdx + Ydy + Zdz) – 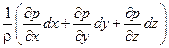 –
– 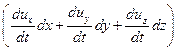 = 0.
= 0.
Т.к. для установившегося течения линии тока совпадают с траекториями движения частиц, то
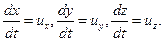
Тогда
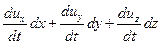 =
= 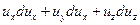 =
= 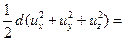
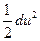
Для установившегося движения давление зависит только от координат, поэтому второй член уравнения есть полный дифференциал давления dp. Получим
(Xdx + Ydy + Zdz) – 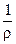 dp – dp – 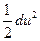 = 0 = 0
| (2.43) |
Мы получили дифференциальное уравнение движения невязкой жидкости.
В поле силы тяжести
X = 0, Y = 0, Z = – g,
тогда уравнение запишется в следующем виде
– gdz – 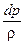 –
– 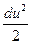 = 0.
= 0.
После интегрирования этого уравнения получаем (при ρ = const) уравнение
gz + 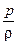 + + 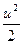 = const, = const,
| (2.44) |
которое называется уравнением Бернулли для струйки невязкой жидкости.
2.2.6. Общее уравнение энергии в интегральной форме
(Уравнение Бернулли для потока реальной жидкости)
Для двух сечений струйки невязкой жидкости это уравнение будет выглядеть следующим образом
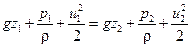 . .
| (2.45) |
Сумма слева представляет полную удельную энергию струйки в сечении 1-1, сумма справа – полную удельную энергию струйки в сечении 2-2. Можно записать, что
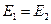 .
.
На практике энергия струйки в начале больше энергии струйки в конце, т.к. часть энергии теряется на преодолении сил вязкости. В процессе движения вязкой жидкости запас ее механической энергии уменьшается, и на самом деле
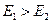 .
.
Обозначим энергию, затрачиваемую на преодоление сил сопротивления Eпот. Eпот – это та часть механической энергии, которая, вследствие вязкости, переходит в тепловую энергию. Другими словами можно сказать, что Eпот – это часть энергии, которая израсходована на преодоление гидравлических сопротивлений.
| Е1 = Е2 + Eпот. | (2.46) |
При выводе уравнения Бернулли для элементарной струйки можно было пренебречь изменением скорости и давления в пределах нормальных сечений благодаря их малым величинам. В потоке жидкости скорости и давления в пределах живых сечений различны, и это необходимо учитывать. Согласно гипотезе Ньютона, жидкость как бы прилипает к стенкам канала, по которому она течет и ее скорость равна нулю. Но с увеличением расстояния от стенки, скорость струек увеличивается. Так называемая мощность потока складывается из энергии отдельных струек
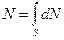 ,
,
где N – мощность потока; dN – мощность струйки; S – площадь живого сечения потока.
Для мощности струйки можно записать:
dN = Ed 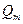 = (gz +
= (gz + 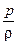 +
+ 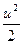 ) ρuds,
) ρuds,
где ds – площадь живого сечения струйки.
Величина удельной энергии потока равна частному от деления мощности потока на массовый расход 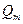
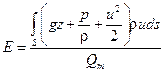 .
.
Это уравнение можно разбить на два интеграла
E = 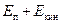 =
= 
 ,
,
где 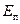 – удельная потенциальная энергия потока относительно выбранной плоскости сравнения;
– удельная потенциальная энергия потока относительно выбранной плоскости сравнения; 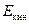 – удельная кинетическая энергия потока.
– удельная кинетическая энергия потока.
Для вычисления 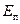 надо знать закон изменения давления по живому сечению. Для плавноизменяющихся течений ускорения и силы инерции незначительны, поэтому ими можно пренебречь. Экспериментально доказано, что в плавноизменяющемся потоке давления распределяются по закону гидростатистики gz
надо знать закон изменения давления по живому сечению. Для плавноизменяющихся течений ускорения и силы инерции незначительны, поэтому ими можно пренебречь. Экспериментально доказано, что в плавноизменяющемся потоке давления распределяются по закону гидростатистики gz 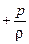 = const.
= const.
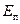 = = 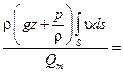 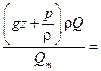 gz gz 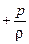 . .
| (2.47) |
Для вычисления интеграла  нужно знать закон распределения скоростей по сечению. Умножим и поделим это выражение на
нужно знать закон распределения скоростей по сечению. Умножим и поделим это выражение на  .
.

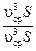 =
= 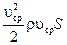
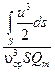 =
= 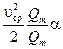 ,
,
где α – коэффициент, который учитывает неравномерность распределения скоростей в сечении, называется коэффициент Кориолиса. Получаем выражение для удельной кинетической энергии потока:
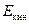 = = 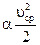 . .
| (2.48) |
Запишем уравнение Бернулли для двух сечений потока реальной жидкости
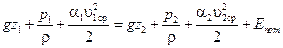 . .
| (2.49) |
Полученное уравнение позволяет сделать следующие выводы:
1. При увеличении кинетической энергии потока от одного сечения к другому потенциальная энергия уменьшается, и, наоборот, с увеличением потенциальной энергии, кинетическая уменьшается.
2. Коэффициент α тем больше, чем больше скорости отдельных струек отличаются от величины средней скорости. Если скорости всех элементарных струек будут равны средней скорости, то α = 1.
Дата добавления: 2015-08-26; просмотров: 1357;
