Уравнение неразрывности. Основным условием, которое должно соблюдаться при течении жидкости, является непрерывность изменения параметров потока в зависимости от координат и времени
Основным условием, которое должно соблюдаться при течении жидкости, является непрерывность изменения параметров потока в зависимости от координат и времени, т.е. при течении жидкости должны быть соблюдены условия при, которых жидкость должна двигаться в канале как сплошная среда, без разрывов.
Выделим внутри пространства с движущейся капельной жидкостью неподвижный контур в форме элементарного параллелепипеда с ребрами dx, dy, dz (см. рис. 2.35). Обозначим скорость жидкости, которая втекает в левую грань параллелепипеда, через 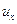 . Скорость жидкости, вытекающей из правой грани, вследствие неразрывности поля скоростей равна
. Скорость жидкости, вытекающей из правой грани, вследствие неразрывности поля скоростей равна
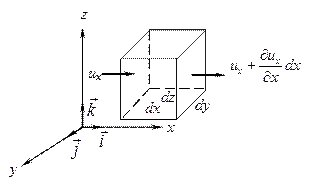
Рис. 2.35. Движение жидкости через контур
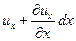 .
.
Поскольку рассматриваемый элементарный объем неподвижен, изменение скорости не зависит от времени. В направлении оси х через левую грань втечет за 1 с жидкость массой 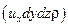 , а вытекает через правую грань
, а вытекает через правую грань
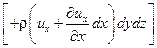 .
.
Значит, за 1 с из параллелепипеда вытекает в направление оси х жидкости больше, чем втекает, на
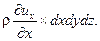
Аналогичные выражения получаются и для направлений x, y, z. Закон сохранения массы требует, чтобы сумма трех полученных приращений была равна нулю:
 . .
| (2.33) |
Это уравнение называют уравнением неразрывности, т.к. оно предполагает, что жидкость является сплошной средой.
Рассмотрим уравнение неразрывности для случая течения струйки при установившемся движении. Масса жидкости течет в трубке тока (см. рис. 2.34). Пусть левое входное сечение трубки тока имеет площадь 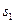 и в этом сечении скорость жидкости
и в этом сечении скорость жидкости 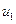 , а ее плотность
, а ее плотность 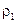 . Площадь сечения на выходе из трубки тока
. Площадь сечения на выходе из трубки тока 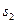 , скорость течения жидкости
, скорость течения жидкости 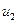 , и ее плотность
, и ее плотность 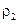 . Скорости струйки направлены по касательной к стенкам трубки тока, поэтому через стенки обмен массой с окружающей жидкостью отсутствует. Через левое сечение втекает в единицу времени масса жидкости
. Скорости струйки направлены по касательной к стенкам трубки тока, поэтому через стенки обмен массой с окружающей жидкостью отсутствует. Через левое сечение втекает в единицу времени масса жидкости 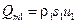 . Через правое сечение вытекает в единицу времени масса жидкости
. Через правое сечение вытекает в единицу времени масса жидкости 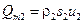 . В трубке тока масса жидкости, находящаяся между левым и правым сечениями, остается постоянной, следовательно, условие сплошности потока в трубке тока будет:
. В трубке тока масса жидкости, находящаяся между левым и правым сечениями, остается постоянной, следовательно, условие сплошности потока в трубке тока будет:
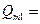 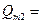 const. const.
| (2.34) |
Если плотность жидкости по длине трубки тока не изменяется, т.е. 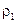 =
= 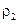 , то можно записать для левого и правого сечений:
, то можно записать для левого и правого сечений:
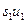 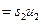 = const или = const или 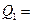 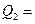 const. const.
| (2.35) |
Полученное уравнение является уравнением неразрывности для трубки тока.
Для потока реальной жидкости уравнение неразрывности записывается в следующем виде:
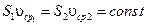 , ,
| (2.36) |
где  и
и 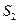 – площади сечения потока в сечениях на входе и на выходе;
– площади сечения потока в сечениях на входе и на выходе; 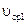 и
и 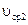 – средние скорости потока в этих сечениях.
– средние скорости потока в этих сечениях.
Можно сделать два важных вывода:
- При установившемся движении жидкости объемный расход не меняется;
- При увеличении площади сечения потока жидкости средняя скорость уменьшается, и, наоборот, при уменьшении сечения - скорость увеличивается.
Дата добавления: 2015-08-26; просмотров: 857;
