Задача 2.2-5, 10
Центробежный насос подает воду с температурой t = 15 °Спо трубе диаметром d = dнмми длиной l = 27 м. Насос создает давление на выходе рн = 2,65 атм и подачу Q = л/с. Определить напор H, создаваемый насосом.
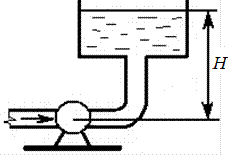
Рис. 2.31. К задаче 2.2-5, 10
Примечание. Потерями напора пренебречь.
Основные понятия кинематики жидкости
Для описания движения жидкости используется математическая модель. В гидравлике наибольшее распространение получила модель Эйлера, суть которой можно объяснить следующим образом. Предположим, что точка М движется по некоторой траектории в системе неподвижных координат. Мгновенное значение составляющих скорости вдоль осей координат будет зависеть от положения точки, т.е. от величины координат x, y, z и времени t. Для составляющих скоростей течения жидкости в рассматриваемой точке 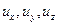 (см. рис. 2.32), можно записать функциональные зависимости:
(см. рис. 2.32), можно записать функциональные зависимости:
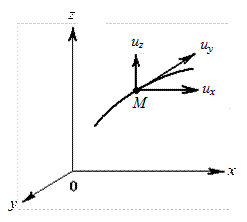
Рис. 2.32. Скорость в точке
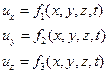
| (2.29) |
Зная для конкретного случая течения значения этих функций, можно для любого момента времени получить распределение скоростей течения жидкости.
Расход – количество жидкости, проходящей в единицу времени через данное сечение трубопровода. Различают объемный и массовый расходы.
Объемный расход – объем жидкости, проходящий в единицу времени через данное сечение трубопровода:
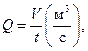
| (2.30) |
где V – объем жидкости.
Массовый расход – масса жидкости, проходящая в единицу времени через данное сечение:
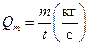 . .
| (2.31) |
Соответственно, 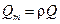 , где ρ – плотность жидкости.
, где ρ – плотность жидкости.
Траектория– кривая, вдоль которой происходит перемещение частицы жидкости.
Линия тока – кривая, в каждой точке которой вектор скорости движения частицы направлен по касательной к ней (см. рис. 2.33).

Рис.2.33. Линия тока
Трубка тока – поверхность, очерченная вдоль небольшого контура внутри которой вдоль линии тока перемещаются частицы жидкости. Стенки трубки тока непроницаемы. Площадь поперечного сечения трубки тока мала, поэтому скорости движения в каждой точке равны (см. рис. 2.34).

Рис. 2.34. Трубка тока
Элементарная струйка – поток жидкости, протекающий в трубке тока Элементарную струйку можно представить также как совокупность линий тока, проходящих через бесконечно малое сечение ds, а разность скоростей соседних линий тока бесконечно мала. Расход элементарной струйки dq = uds. Поток жидкости можно представить как совокупность трубок тока, в которых движутся элементарные струйки.
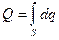 .
.
Средняя скорость потока– скорость, одинаковая в каждой точке потока в данном сечении, соответствует реальному расходу
 ,
,
где  – скорость в точке в данном сечении; i – количество точек.
– скорость в точке в данном сечении; i – количество точек.
Для потока жидкости, состоящего из нескольких трубок тока можно записать
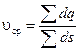 или или 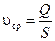 , ,
| (2.32) |
где S – площадь сечения потока жидкости.
Дата добавления: 2015-08-26; просмотров: 1004;
