Вторая основная задача динамики.

По заданным силам и массе точки требуется определить закон движения.

Вторая основная задача связана с интегрированием. В соответствии с этим можно говорить и об относительной сложности этих задач. Обычно вторая основная задача значительно сложнее первой.

Второй закон Ньютона можно записать в виде системы дифференциальных уравнений второго порядка:

,

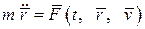или в проекциях на оси декартовой системы координат

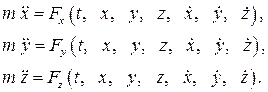
Для нахождения уравнений движения точки нужно дважды проинтегрировать эти уравнения. Как известно, при интегрировании дифференциального уравнения второго порядка, решение содержит две константы интегрирования, т.е. для случая трех уравнений имеется шесть произвольных постоянных. Подставляя найденные значения констант интегрирования в общее решение дифференциальных уравнений движения, получим частные решения, справедливые для данных в задаче начальных условий:

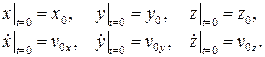
С учетом принятых обозначений эти решения примут вид

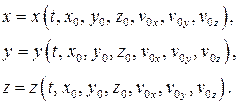
Заметим, что под действием одной системы сил точка может совершать целый класс движений, определяемых начальными условиями.

Если каким-либо образом удалось сразу получить первые интегралы, то дальнейшее решение задачи сводится к однократному интегрированию трёх дифференциальных уравнений первого порядка.