Дифференциальные уравнения движения материальной точки

Пусть материальная точка движется под действием приложенных к ней сил. Подставив во второй закон Ньютона ускорение в виде второй производной по времени от радиус-вектора, получим дифференциальное уравнение движения материальной точки

.

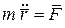Проектируя это векторное уравнение на координатные оси декартовой системы координат, получим дифференциальные уравнения движения точки

.

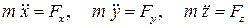В случае прямолинейного движения точки имеем только одно уравнение

.

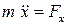Уравнения движения в проекциях на оси естественных координат имеют вид

.

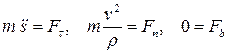Основное уравнение динамики точки остается справедливым и для несвободной материальной точки, на которую наложены связи. В этом случае, в число действующих на точку сил, следует включить и силы реакций связей.