Динамика несвободной материальной точки
Как уже говорилось ранее, основной закон динамики для несвободной материальной точки, а следовательно, и ее дифференциальные уравнения движения имеют такой же вид, как и для свободной точки. В этом случае к действующим на точку силам необходимо добавить силы реакций связей.
Пусть материальная точка движется по заданной гладкой неподвижной поверхности, уравнение которой в декартовой системе координат задано выражением 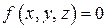 . Применяя принцип освобождаемости от связей, и составляя основное уравнение динамики несвободной точки, получим:
. Применяя принцип освобождаемости от связей, и составляя основное уравнение динамики несвободной точки, получим:
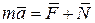 ,
,
где 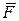 — равнодействующая активных сил, действующих на точку,
— равнодействующая активных сил, действующих на точку, 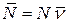 — неизвестная реакция связи, действующая по внешней нормали к поверхности.
— неизвестная реакция связи, действующая по внешней нормали к поверхности.
Проектируя это уравнение на оси декартовой системы координат, получаем дифференциальные уравнения движения точки по гладкой поверхности:
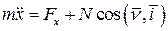 ,
, 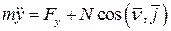 ,
, 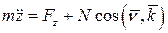
Из дифференциальной геометрии известно, что выражение единичного вектора внешней нормали 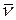 к поверхности определяет вектор – градиент, задаваемый формулой
к поверхности определяет вектор – градиент, задаваемый формулой
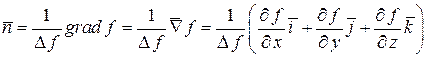 ,
,
где 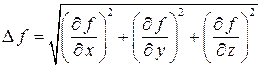 — модуль вектор – градиента
— модуль вектор – градиента 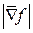
Поэтому направляющие косинусы вектора 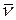 и, следовательно, нормальной реакции опоры
и, следовательно, нормальной реакции опоры 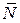 к поверхности
к поверхности 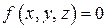 определяются выражениями:
определяются выражениями:
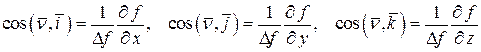 .
.
С учетом последних формул уравнения движения несвободной точки перепишутся в виде:

где 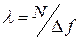 — множитель Лагранжа.
— множитель Лагранжа.
Полученные дифференциальные уравнения — уравнения Лагранжа первого рода для несвободной материальной точки; вместе с уравнением связи 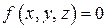 позволяют определить четыре неизвестные
позволяют определить четыре неизвестные 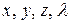 как функции времени
как функции времени 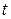 . Алгебраическое значение нормальной реакции находится затем по формуле
. Алгебраическое значение нормальной реакции находится затем по формуле 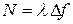 .
.
При движении материальной точки по негладкой поверхности, кроме нормальной реакции возникает сила трения 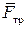 , направленная против вектора скорости точки, величину которой можно определить векторным выражением
, направленная против вектора скорости точки, величину которой можно определить векторным выражением
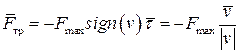 ,
,
где 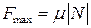 — предельное значение силы трения,
— предельное значение силы трения, 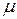 — коэффициент трения.
— коэффициент трения.
Дифференциальные уравнения движения точки в этом случае запишутся в виде
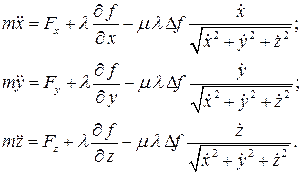
При движении точки по заданной гладкой пространственной кривой необходимо учесть, что кривую линию в пространстве можно рассматривать как геометрическое место пересечения двух поверхностей 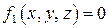 и
и 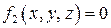 .
.
Эти поверхности создадут для движущейся точки две нормальные реакции  и
и 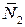 , и поэтому полная нормальная реакция пространственной кривой
, и поэтому полная нормальная реакция пространственной кривой 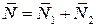 . Дифференциальные уравнения Лагранжа первого рода в этом случае примут вид
. Дифференциальные уравнения Лагранжа первого рода в этом случае примут вид
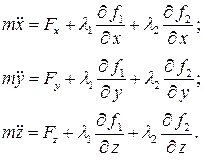
где соответственно
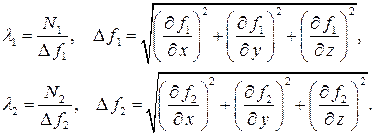
Совместно с двумя уравнениями поверхностей получаем пять уравнений для определения пяти неизвестных величин 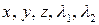 как функции времени.
как функции времени.
При движении точки по плоской кривой удобно использовать естественную систему координат. Проектируя векторное уравнение на оси 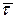 и
и 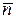 (касательную и главную нормаль к траектории), получим
(касательную и главную нормаль к траектории), получим
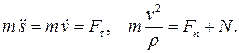
Эти уравнения называются уравнениями движения несвободной точки в форме Эйлера. Уравнения движения несвободной точки в форме Эйлера с учётом трения запишутся в виде:
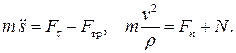
Добавив к ним закон Кулона  , будем иметь систему уравнений, достаточную для определения закона движения
, будем иметь систему уравнений, достаточную для определения закона движения 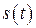 и сил
и сил 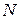 и
и 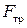 .
.
Дата добавления: 2015-08-08; просмотров: 2844;
