Сила веса и сила тяжести.

Найдем условия относительного равновесия материальной точки на поверхности Земли, принимая во внимание ее вращение с постоянной угловой скоростью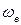

.

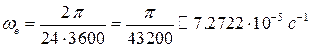Рис. 3. 2 Относительное равновесие точки

На эту точку действуют: сила тяготения 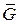(рис. 3. 2), перпендикулярная поверхности геоида, форма которого близка к сфере, поэтому можно считать силу 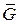направленной к центру Земли; переносная сила инерции 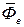, а также реакция опорной поверхности 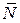. В соответствие с условием относительного равновесия, получим

.

где 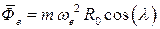— центробежная сила инерции,

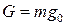— сила тяжести.

Таким образом, вес точки равный 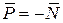будет определяться выражением 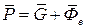, то есть он является равнодействующей двух сил: тяготения и центробежной силой инерции.

Оценим, насколько вес точки отличается от величины силы тяготения. Обозначим геоцентрическую широту, т.е. угол между осью 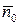и плоскостью экватора через 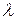, а географическую широту, т.е. угол между осью 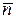и той же плоскостью, через 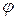. Проектируя уравнение на оси 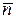и

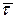
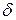и учитывая, что , получим систему двух уравнений относительно и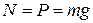

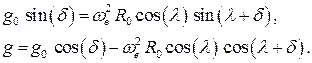
Учитывая, что угол 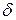очень мал, решение первого уравнения данной системы можно представить в виде

а выражение для величины будет иметь следующий вид

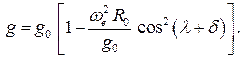
Так как вес тела (материальной точки) должен быть направлен по нормали к поверхности, то угол 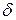, задающий ориентацию внешней нормали, определяет степень отклонения реальной поверхности Земли от идеальной сферы. Как уже отмечалось, Земля имеет форму геоида, который в первом приближении заменяется близким к нему однородным эллипсоидом вращения с полуосями: большой (экваториальный радиус) 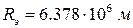и малой (полярный радиус) 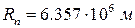. Поэтому при изучении высокоточных задач: движение искусственных спутников, баллистических ракет, приливных течений и т.д. необходимо учитывать несферичность Земли.

Поскольку отличие полярного радиуса Земли от экваториального незначительно, и составляет всего 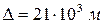, то Землю в достаточно близком приближении можно считать равновеликой по объему и массе 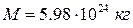сферой радиуса 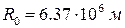. Тогда, согласно всемирному закону тяготения Ньютона, сила тяжести 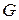будет равна

,

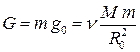где 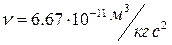— гравитационная постоянная.

Подставляя числовые значения констант, найдем величину ускорения свободного падения для не вращающейся сферической Земли, а также выражение для угла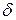

.

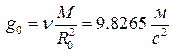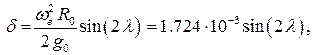
Пренебрегая величиной 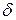в выражении , задающем ускорение свободного падения , с учетом вращения Земли, получим

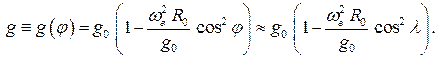
При решении задач динамики составного движения обычно считают Землю сферой радиуса 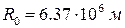, на которой ускорение свободного падения определяется формулой .