ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ

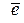Пусть на тело действует система параллельных сил. Введём единичный вектор , параллельный линии действия сил системы. .

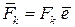Приведём систему сил к центру С, пользуясь основной теоремой статики. Тогда главный вектор и главный момент системы можно записать в виде:

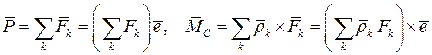
Рассмотрим случай, когда главный вектор 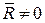, а главный момент 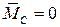. Система в этом случае приводится к равнодействующей. Точка приложения равнодействующей называется центром параллельных сил. Для определения положения этой точки применим теорему Вариньона о моменте равнодействующей

Преобразуя это выражение, получим .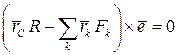

Откуда

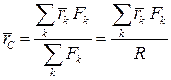или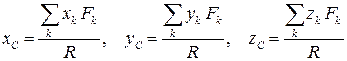

ЦЕНТР ТЯЖЕСТИ ОБЪЁМА, ПЛОЩАДИ, ЛИНИИ

Сила, с которой тело притягивается к Земле, называется силой тяжести. Точка приложения этой силы — центром тяжести. Поскольку силы тяжести действуют на каждую частицу тела, то её надо считать распределённой. При небольших (по сравнению с Землей) размерах тела силы тяжести с большой степенью точности можно считать параллельными. Для определения равнодействующей и точки приложения силы тяжести разобьём тело на " 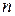" достаточно малых элементов. Предельным переходом, устремляя 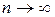, получим точные формулы.

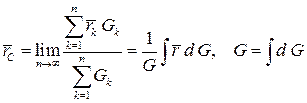
Вес элементарного объема можно выразить через удельный вес 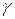формулой 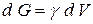. При вычислении центра тяжести пластинки постоянной толщины 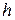его элементарный объём можно представить в виде 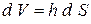. При вычислении элементарного объёма стержня можно воспользоваться соотношением 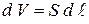, где 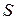— площадь поперечного сечения стержня.

Тогда формулы для определения центра тяжести плоской фигуры

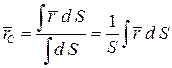
криволинейного стержня (линии)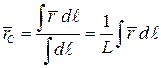

Динамика

Динамика — раздел механики, в котором изучается движение материальных объектов в зависимости от действующих на них сил. Простейшим материальным объектом является материальная точка. Это модель материального тела любой формы, размерами которого в рассматриваемых задачах можно пренебречь и принять за геометрическую точку, имеющую определенную массу. Более сложные материальные объекты — механические системы и сплошные тела — считают состоящими из материальных точек.

Сила считается в механике основным, первичным понятием. Свойства сил, приложенных к твердому телу и точке, рассматривались в статике. В динамике силы оцениваются по их динамическому действию, т.е. по изменению ими характеристик движения материальных объектов.

Движение материальных объектов следует рассматривать относительно определенной системы отсчета. Оно совершается в пространстве с течением времени. В классической механике пространство считается трехмерным эвклидовым пространством, свойства которого не зависят от движущихся в нем материальных объектов. Время в классической механике инвариантно по отношению к выбору системы координат.

В основу классической механики положены законы или аксиомы Ньютона, которые были получены им путём обобщений целого ряда опытных данных и теоретических исследований.

ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

Задачи динамики материальной точки можно разделить на три раздела:

· Динамика свободной материальной точки;

· Динамика несвободной материальной точки;

· Динамика относительного движения материальной точки.