Следствие 1
Если исходная матрица квадратная m= n, то мы получаем, что определитель её равен нулю ⇔система её столбцов линейно зависимая.
Получаем критерий равенства нуля определителя.
Вспомним свойство определителя, как транспонирование.
При транспонирование определитель не меняется.
Определитель – ранг матрицы – ранг системы её столбцов
Определитель – наивысший порядок отличен от 0
Определитель – ранг системы её строк
Способы вычисления рангов:
1) Метод окаймляющих миноров
2) Метод элементарных преобразований
Алгоритм:
1. Смотрим, перебираем все миноры 1-го порядка:
а) все они 0 ⇒матрица нулевая, ранг = 0
б) Существует по крайней мере один не нулевой минор, ранг не меньше 1.
2. Перебираем все миноры 2 порядка:
а) все миноры 2-го порядка 0, то ранг = 1
б) среди миноров 2-го порядка есть не нулевой, ранг≥2
3. ……( и т.д. перебирать)
Но метод №1 надо перебирать на 2 шаге не все миноры, а окаймляющие, тот минор не нулевого порядка(т.д. надо рассматривать только лишь окаймляющие найденного не нулевого минора).
Пример на метод окаймления:
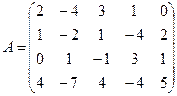 1) Существует минор 1-го порядка, например 𝑎11=2≠0 ⇒r≥1
1) Существует минор 1-го порядка, например 𝑎11=2≠0 ⇒r≥1
2)
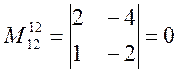
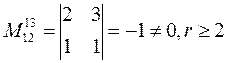
3)
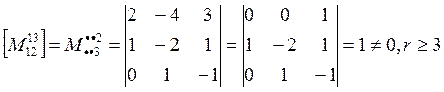
Теорема:С помощью элементарных преобразований систем векторов строк и векторов столбцов.
Всегда можно получить единичную матрицу, порядок которой равен рангу исходной матрицы.
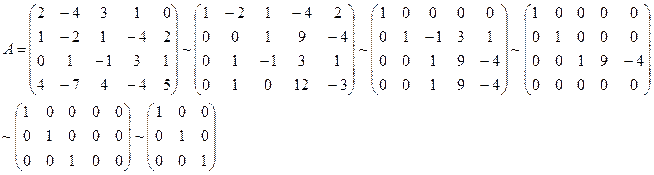
Дата добавления: 2015-07-24; просмотров: 730;
