Важнейший случай СЛАУ.
Однородные СЛАУ – называется однородной, если все её свободные члены нули( столбцов свободных членов 0).
|
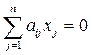
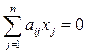
1≤i ≤m
|
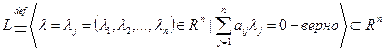
|
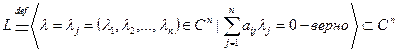
L– множество решений однородной СЛАУ(1).
Теорема о Lподпространство в Rn
Сумма любых двух решений вновь решение.
λ=(λj) и β=(βj)∊L
γ=λ+β=(γj=λj+βj)⇒
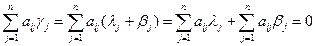
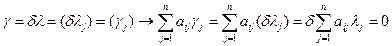
Система совместна всегда, так как есть всегда 0 решений.
Теорема о базисе и размерности пространства решений однородной СЛАУ.
Пусть задана произвольная однородная СЛАУ(1).
1) r=rangA=rang(αij) (r≤m)
2) фиксируем ранговый минор, не ограничивая общности.
3) Разбиваем на 2 группы
x1, x2,…, xr- основные
xr+1, xr+2,…, xn- свободные
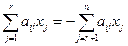
1≤i≤r, n≤m
| xr+1 | xr+2 | . | . | xn | |
| λ1 | λ1,r+1 | λ1,r+2 | . | . | λ1,n |
| λ2 | λ2,r+1 | λ2,r+2 | . | . | λ2,n |
| . | . | . | . | . | . |
| . | . | . | . | . | . |
| λn-r | λn-r,r+1 | λn-r,r+2 | . | . | λn-r,n |
n-r– серия свободных неизвестных, определитель должен быть отличен от нуля.
λ 1=(λ1,1,…, λ1,r, λ1,r+1,…, λ1,n)∊L
λ 2=(λ2,1,…, λ2,r, λ2,r+1,…, λ2,n)∊L
…………………………………
λ n-r=(λn-r,1,…, λn-r,r, λn-r,r+1,…, λn-r,n)∊L
Пусть β – произвольные решения
β =(β1,…, βr, βr+1,…, βn), где (β1,…, βr) – основные, (βr+1,…, βn) – свободные.
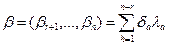
Пример:
dimL1
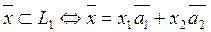
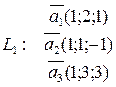
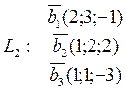
rangL1=2
rangL2=2
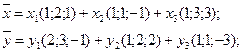
Связь решений произвольной СЛАУ и её приведенной однородной.
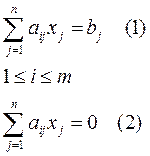
Теорема 1.Разность любых двух решений СЛАУ(1) будет решением её приведенной системы.
Теорема 2.Сумма любого частного решения системы(1) и любого решения системы(2) является частным решением системы(1).
Теорема 3.Сумма любого частного решения системы(1) и общего решения его приведенной системы(2) является общим решением системы(1).
Дата добавления: 2015-07-24; просмотров: 747;
