Фдз 9. Линейные, билинейные и квадратичные функции и формы в линейном пространстве.

1. Какие из приведенных ниже функций, заданных на линейном векторном пространстве 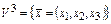, являются линейными?

1.1. 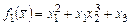, 1.2. 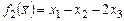, 1.3. .

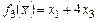2. Найти матрицы приведенных ниже билинейных форм и записать их в матричном виде.

2.1. , .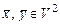

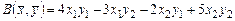2.2. , .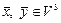

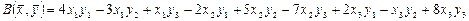2.3. , .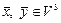

3. Считая, что билинейные формы в примерах 2.2, 2.3 заданы в базисе 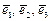, найти матрицы и матричную запись этих форм в новом базисе 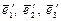, где .

4. Найти квадратичные формы, соответствующие билинейным формам

примеров 2.1, 2.2, 2.3. Найти матрицы этих квадратичных форм и записать квадратичные формы в матричном виде.

5. Найти симметричные билинейные формы, соответствующие квадратичным формам из примера 4, и записать их в матричном виде.

__________________________________________________________

Домашнее задание.

1. Билинейные формы 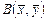, 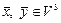в базисе 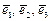имеет вид

1.1. .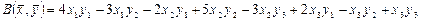

1.2. .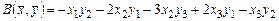

Найти матрицу билинейной формы, ее матричное представление, а также матрицу и выражение 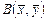в новом базисе .

2. Найти квадратичные формы, соответствующие билинейным формам

из примеров 1.1, 1.2. Записать эти квадратичные формы в матричном виде. По квадратичным формам записать соответствующие им симметричные билинейные формы.

_________________________________________________________________________

Фдз 10. Канонический и нормальный вид квадратичной формы. Метод Лагранжа приведения квадратичной формы к каноническому виду. Положительный и отрицательный индексы, ранг квадратичной формы. Закон инерции. Три инварианта квадратичной формы.

1. Найти матрицу и матричное представление следующих квадратичных форм.

1.1. ,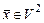

1.2. , .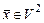

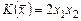1.3. , .

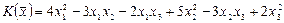1.4. , .

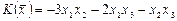2. Методом Лагранжа привести к каноническому виду квадратичные формы из задания 1 и выписать соответствующие невырожденные преобразования координат, приводящие квадратичные формы к каноническому виду. Найти ранг и индексы инерции данных квадратичных форм.

3. Найти нормальный вид рассмотренных квадратичных форм из задания 1. _______________________________________________________________________

Домашнее задание.

1. Методом Лагранжа привести к каноническому виду квадратичные формы, приведенные ниже и привести невырожденные преобразования координат, приводящие квадратичные формы к каноническому виду.

1.1. , .

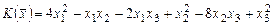1.2. , .

__________________________________________________________________________

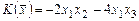Выполнить следующие пункты «своих» задач из Типового расчета:

Задача 8. 1).