Домашнее задание

1. Исходя из геометрии действия линейного оператора, найти собственные векторы и собственные значения следующих линейных операторов:

1.1. Оператора проектирования векторов на плоскость ;

1.2. Оператора отражения векторов от оси ;

1.3. Оператора поворота векторов на вокруг оси .

2. Используя определение собственного вектора и собственного значения оператора найти собственные векторы и собственные значения следующих линейных операторов.

2.1. , , .

2.2. , , .

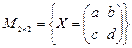2.3. , .

Решить «свою» задачу 4 из Типового расчета:

Фдз 7. Собственные значение и собственные векторы оператора, матрицы.

1. Привести алгоритм нахождения собственных значений и собственных векторов по матрице оператора.

2. Записать характеристическую матрицу и характеристическое уравнение для матриц:

2.1. ; 2.2. ; 2.3. .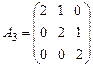

3.. Найти собственные значения и собственные векторы матриц

3.1. , 3.2. , 3.3. .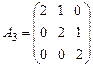

3. Найти собственные значения и собственные векторы линейного оператора , где 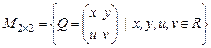, и оператор 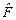действует по правилу , где . Провести решение с помощью матрицы оператора в стандартном базисе 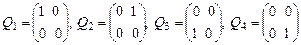пространства .

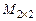4. Найти собственные значения и собственные векторы линейного оператора , где , и оператор 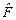действует по правилу .

Провести решение с помощью матрицы оператора в стандартном базисе пространства .

______________________________________________________________________

Домашнее задание.

1. Найти собственные значения и собственные векторы матриц

1.1. 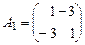, 1.2. 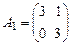, 1.3. .

2. Найти собственные значения и собственные векторы линейного оператора , где , и оператор 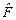действует по правилу . Провести решение с помощью матрицы оператора в стандартном базисе пространства .

_________________________________________________________________

Выполнить следующие пункты из «своих» задач Типового расчета:

Задача 6. 4).