Домашнее задание.
1. Доказать линейность оператора 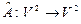 , если в базисе
, если в базисе 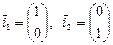 действие этого оператора производится по формулам
действие этого оператора производится по формулам 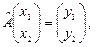 где
где 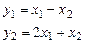 . Найти матрицу этого оператора в базисе
. Найти матрицу этого оператора в базисе 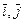 и в базисе
и в базисе 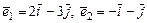 .
.
2. Доказать, что отображение 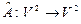 ,
, 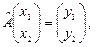
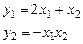 является оператором, но не является линейным оператором.
является оператором, но не является линейным оператором.
3. Доказать, что оператор  ,
,  ,
, 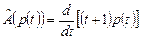 является линейным и найти матрицу этого оператора в стандартном базисе
является линейным и найти матрицу этого оператора в стандартном базисе 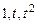 и базисе
и базисе 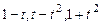 .
.
Выполнить следующие пункты из «своих» задач Типового расчета:
Задача 5. 1),2)
Задача 6. 1),2).
Фдз 5. Действия с линейными операторами. Образ, ядро, ранг, дефект линейного оператора.
1. Даны два линейных оператора  , действующие в одном и том же линейном пространстве
, действующие в одном и том же линейном пространстве 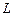 . Дать определения для операторов:
. Дать определения для операторов:
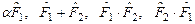 .
.
2. Даны два линейных оператора 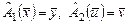 , действующие в пространстве
, действующие в пространстве 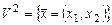 по следующим правилам:
по следующим правилам: 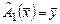 , где
, где  ;
;
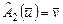 , где
, где 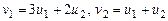 . Найти матрицы операторов
. Найти матрицы операторов 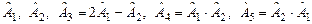 в базисе
в базисе 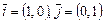 .
.
3. Дать определение ядра, ранга и дефекта линейного оператора.
4. Исходя из определений и геометрических свойств оператора 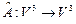 , найти его ядро и образ в следующих случаях, указать также ранг и дефект.
, найти его ядро и образ в следующих случаях, указать также ранг и дефект.
4.1. 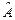 - оператор проектирования векторов на плоскости
- оператор проектирования векторов на плоскости 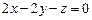 ;
;
4.2. 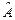 - оператор проектирования на ось
- оператор проектирования на ось 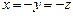 ;
;
4.3. 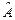 - оператор поворота векторов на
- оператор поворота векторов на 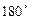 вокруг оси
вокруг оси  .
.
5. Найти ядро, образ, ранг и дефект следующих линейных операторов.
5.1. 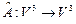 ,
, 
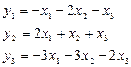 .
.
5.2.  ,
,  ,
, 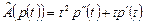 .
.
5.3.  ,
, 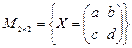 ,
, 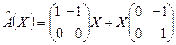 .
.
6. Дать определение обратного оператора 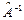 данному линейному оператору
данному линейному оператору 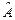 .
.
7. Указать, в каких случаях из приведенных выше примеров 4,5,6 оператор 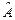 является невырожденным и допускает обратный оператор
является невырожденным и допускает обратный оператор 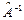 . Найти матрицы этих обратных операторов.
. Найти матрицы этих обратных операторов.
__________________________________________________________________________
Домашнее задание.
1. Найти ядро, образ, ранг и дефект линейного оператора
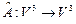 ,
, 
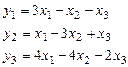 .
.
Допускает ли данный оператор обратный оператор 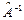 ?
?
2. Найти ядро, образ, ранг и дефект линейного оператора 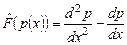 ,
,
действующего в линейном пространстве  .
.
Выполнить следующие пункты из «своих» задач Типового расчета:
Задача 5. 4).
Задача 6. 3).
Фдз 6. Собственные значение и собственные векторы линейного оператора.
1. Дать определение собственного вектора и собственного значения линейного оператора.
Указать геометрический смысл собственного вектора.
2. Исходя из геометрии действия линейного оператора, найти собственные векторы и собственные значения следующих линейных операторов.
2.1. Оператора отражения векторов относительно плоскости 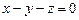 ;
;
2.2. Оператора проектирования на ось 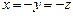 ;
;
2.3. Оператора поворота векторов на 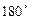 вокруг оси
вокруг оси  .
.
3. Используя определение собственного вектора и собственного значения оператора найти собственные векторы и собственные значения следующих линейных операторов.
3.1. 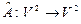 ,
, 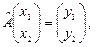
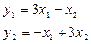 .
.
3.2. 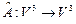 ,
,  .
.
3.3.  ,
,  ,
,  .
.
3.4.  ,
, 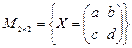 ,
, 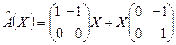 .
.
________________________________________________________________________
Дата добавления: 2015-07-30; просмотров: 1587;
