Домашнее задание. 1. Исследовать на линейную зависимость систему матриц
1. Исследовать на линейную зависимость систему матриц
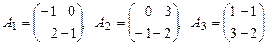 .
.
2. Доказать, что множество 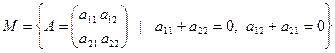 является линейным подпространством в пространстве
является линейным подпространством в пространстве 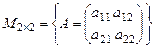 . Найти базис и размерность подпространства
. Найти базис и размерность подпространства 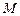
Фдз 2. Закон преобразования координат вектора при переходе к новому базису. Матрица перехода от старого базиса к новому базису. Ранг матрицы. Критерий совместности линейной системы (теорема Кронекера-Капелли).
1. Записать в матричном виде переход от базиса  к новому базису
к новому базису 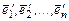 в
в  -мерном линейном пространстве.
-мерном линейном пространстве.
2. Записать в матричном и координатном виде закон преобразования координат вектора при переходе к новому базису.
3. Записать матрицу перехода от базиса 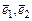 к новому базису
к новому базису 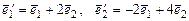 двумерного линейного пространства. Записать в матричном и координатном виде закон преобразования координат вектора при переходе от базиса
двумерного линейного пространства. Записать в матричном и координатном виде закон преобразования координат вектора при переходе от базиса 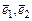 к базису
к базису 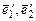 . Найти координаты вектора
. Найти координаты вектора 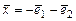 в базисе
в базисе 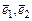 и базисе
и базисе 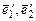
4. Записать матрицу перехода от базиса 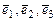 к базису
к базису  трехмерного линейного пространства. Записать в матричном и координатном виде закон преобразования координат вектора при переходе от базиса
трехмерного линейного пространства. Записать в матричном и координатном виде закон преобразования координат вектора при переходе от базиса 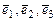 к базису
к базису 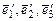 . Найти координаты вектора
. Найти координаты вектора 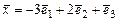 в базисе
в базисе 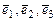 и базисе
и базисе 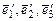 .
.
5. Записать матрицу перехода от стандартного базиса 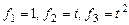 пространства
пространства  к базису
к базису 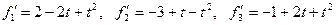 трехмерного линейного пространства. Найти координаты многчлена
трехмерного линейного пространства. Найти координаты многчлена  в базисе
в базисе 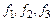 и базисе
и базисе 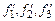 .
.
6. Найти ранг матриц 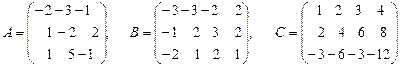 .
.
7. Исследовать на совместность (с помощью теоремы Кронекера-Капелли) системы
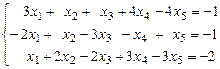 ,
, 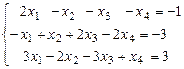 .
.
________________________________________________________________________________
Дата добавления: 2015-07-30; просмотров: 1455;
