Фдз 4. Отображение множеств. Образ, прообраз. Линейный оператор и его матрица.
1. Дано отображение 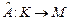 (где
(где 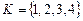 ,
, 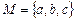 ) по следующему закону:
) по следующему закону:
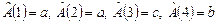 . Найти образы множеств
. Найти образы множеств 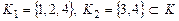 и прообразы для элементов
и прообразы для элементов  . Является ли заданное отображение однозначным, взаимно-однозначным, имеет ли оно обратное отображение?
. Является ли заданное отображение однозначным, взаимно-однозначным, имеет ли оно обратное отображение?
2. Дать определения оператора, линейного оператора.
3. Дано отображение 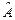 , действующее на множестве
, действующее на множестве  по правилу
по правилу
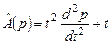 . Показать, что это отображение является оператором, но не является линейным оператором.
. Показать, что это отображение является оператором, но не является линейным оператором.
4. Доказать, что отображение 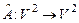 , где
, где 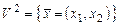 , действующее по правилу
, действующее по правилу 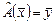 , где
, где 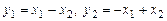 , является линейным оператором.
, является линейным оператором.
Найти образ вектора 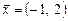 и образ всего пространства
и образ всего пространства 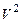 . Исходя из образа пространства
. Исходя из образа пространства 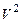 , ответить на вопросы: является ли заданное отображение однозначным, взаимно-однозначным, имеет ли оно обратное отображение?
, ответить на вопросы: является ли заданное отображение однозначным, взаимно-однозначным, имеет ли оно обратное отображение?
5. Доказать линейность оператора 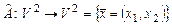 , если в базисе
, если в базисе 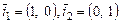 действие этого оператора производится по правилу
действие этого оператора производится по правилу 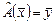 , где
, где 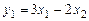 ,
, 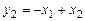 .
.
Найти матрицу этого оператора в базисе 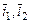 и в базисе
и в базисе 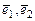 , где
, где 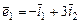 .
. 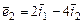 .
.
6.  ,
,  ,
, 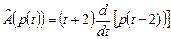 . Доказать линейность оператора
. Доказать линейность оператора 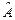 . Найти его матрицу в каноническом базисе
. Найти его матрицу в каноническом базисе 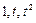 и в базисе
и в базисе 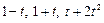 .
.
7. Линейный оператор 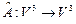 является:
является:
а) оператором отражения векторов от плоскости 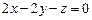 ;
;
б) оператором проектирования на ось 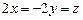 ;
;
в) поворотом векторов на 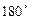 вокруг оси
вокруг оси 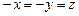 .
.
Исходя из геометрических свойств указанных операторов, найти их матрицы в подходящих базисах и затем в базисе 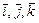 .
.
__________________________________________________________________________
Дата добавления: 2015-07-30; просмотров: 1089;
