Аксиоматическое определение операторов языка программирования в терминах wp.

Определим слабейшее предусловие для основных операторов: оператора присваивания, составного оператора, оператора выбора и оператора цикла.

Оператор присваивания имеет вид: x := E, где x - простая переменная, E – выражение (типы x и E совпадают).

Определим слабейшее предусловие оператора присваивания как Q = wp(x := E, R), где Q получается из R заменой каждого вхождения x на E, что обозначим Q = R^x_Е.

Предполагается, что значение Е определено и вычисление выражения Е не может изменить значения ни одной переменной. Последнее ограничение запрещает функции с побочным эффектом. Следовательно, можно использовать обычные свойства выражений такие, как ассоциативность, коммутативность и логические законы.

Составной оператор имеет вид: begin S₁; S₂; ... ; S_n end

Определим слабейшее предусловие для последовательности двух операторов:

wp(S₁;S₂, R) = wp(S₁, wp(S₂, R)).

Аналогично слабейшее предусловие определяется для последовательности из n операторов.

Оператор выбора определим так:if B₁ → S₁ П B₂ → S₂ ... П B_n → S_n fi

Здесь n ³ 0, B₁, B₂, ..., B_n - логические выражения, называемые охранами, S₁, S₂, ..., S_n - операторы, пара B_i → S_i называется охраняемой командой, П - разделитель, if и fi играют роль операторных скобок.

Выполняется оператор следующим образом.

Проверяются все B_i. Если одна из охран не определена, то происходит аварийное завершение. Далее, по крайней мере, одна из охран должна иметь значение истина, иначе выполнение завершается аварийно.

Выбирается одна из охраняемых команд B_i → S_i, у которой значение B_i истина, и выполняется S_i.

Определим слабейшее предусловие:

wp(if, R) = BB AND (B₁ => wp(S₁, R)) AND ... AND(B_n => wp(S_n, R)),

где BB = B₁ OR B₂ OR ... OR B_n.

Предполагается, что охраны являются всюду определенными функциями (значение их определено во всех состояниях).

Естественно определить wp(if, R) с помощью кванторов:

wp(if, R) = ($ i: 1 i n : B_i) AND("i: 1 i n : B_i => wp(S_i, R)).

Пример 2.4. Определить z = |x|.

С использованием оператора выбора :if x ³ 0 → z := x П x 0 → z := -x fi.

К особенностям оператора выбора следует отнести, во-первых, тот факт, что он включает условный оператор (if... then..), альтернативный оператор (if… then... else...) и оператор выбора (case).

Во-вторых, оператор выбора не допускает умолчаний, что помогает при разработке сложных программ, так как каждая альтернатива представлена подробно, и возможность что-либо упустить уменьшается.

В-третьих, благодаря отсутствию умолчаний, запись оператора выбора представлена в симметричном виде.

Оператор цикла. В обозначениях Э. Дейкстры цикл имеет вид: do B → S od.

Обозначим это соотношение через DO и представим его в следующем виде:

DO: do B₁ → S₁ П B₂ → S₂ ... П B_n → S_nod,

где n ³ 0, B_i → S_i - охраняемые команды.

Выполняется оператор следующим образом. Пока возможно выбирается охрана B_i со значением истина, и выполняется соответствующий оператор S_i. Как только все охраны будут иметь значение ложь, выполнение DO завершится.

Выбор охраны со значением истина и выполнение соответствующего оператора называется выполнением шага цикла. Если истинными являются несколько охран, то выбирается любая из них.

Следовательно, оператор DO эквивалентен оператору

do BB → ifB₂ → S₁ П B₂ → S₂ ... П B_n → S_nfi od или do BB → IF od,

где BB - дизъюнкция охран, IF- оператор выбора.

Пример 2.5. Алгоритм Евклида.

Вариант 1.

задать (N, M);

if N > 0 AND M > 0 → n, m := N, M;

do n ≠ m → if n > m → n := n – m П m > n → m := m – n fi od;

выдать (n)

fi.

Вариант 2.

задать (N, M);

if N > 0 AND M > 0 → n, m := N, M;

do n > m → n := n – m П m > n → m := m – n od;

выдать (n)

fi.

Дадим формальное определение слабейшего предусловия для оператора цикла DO.

Пусть предикат H₀(R) определяет множество состояний, в которых выполнение DO завершается за 0 шагов (в этом случае все охраны с самого начала ложны, после завершения R имеет значение истина):

H₀(R) = NOT BB AND R.

Другими словами, требуется, чтобы оператор цикла DO завершил работу, не производя выборки охраняемой команды, что гарантируется первым конъюнктивным членом предиката H₀(R): NOT BB = T. При этом истинность R до выполнения DO является необходимым условием для истинности R после выполнения DO.

Определим предикат H_k(R) как множество состояний, в которых выполнение DOзаканчивается за k шагов при значении R истина (H_k(R) будет определяться через H_k-1(R)):

H_k(R) = H₀(R) OR wp(IF, H_k-1(R)), k > 0 → wp(DO, R) = ($ k: k ³ 0: H_k(R)).

Это значит, что должно существовать такое значение k, что потребуется не более чем k шагов, для обеспечения завершения работы в конечном состоянии, удовлетворяющем постусловию R.

Определение DO. Если предикаты H_k(R) задаются в виде

H_k(R) = NOT B ANDR, k = 0,

H_k(R) = wp(IF, H_k-1(R)), k > 0, → wp(DO, R)=($ k: k ³ 0: H_k(R)).

Основная теорема для оператора цикла. Пусть оператор выбора IF и предикат P таковы, что для всех состояний справедливо

(P ANDBB) => wp(IF, R).(2.3)

Тогда для оператора цикла справедливо:

(P AND wp(DO, T)) => wp(DO, P AND NOT BB).

Эта теорема известна как основная теорема инвариантности для цикла. Предикат Р, истинный перед выполнением и после выполнения каждого шага цикла, называется инвариантным отношением или просто инвариантом цикла. В математике термин «инвариантный» означает не изменяющийся под воздействием совокупности рассматриваемых математических операций.

Поясним смысл теоремы. Условие (2.3) означает, что если предикат P первоначально истинен и одна из охраняемых команд выбирается для выполнения, то после ее выполнения P сохранит значение истинности. После завершения оператора, когда ни одна из охран не является истиной, будем иметь:

P AND NOTBB.

Работа завершится правильно, если условие wp(DO, T) справедливо и до выполнения DO. Так как любое состояние удовлетворяет T, то wp(DO, T) является слабейшим предусловием для начального состояния такого, что запуск оператора цикла DO приведет к правильно завершаемой работе.

Доказательство.

Из определения DO следует:

H₀(T) = NOT BB ANDT, k = 0;

H_k(T) = wp(IF, H_k-1(T)), k > 0, → wp(DO, T) = ($ k: k ³ 0: H_k(T));

H₀(P AND NOT BB) = P AND NOT BB;

H_k(P AND NOT BB) = wp(IF, H_k-1(P AND NOT BB), → wp(DO, P AND NOT BB) = = ($ k ³ 0: H_k(P AND NOT BB)).

С помощью метода математической индукции можно доказать, что из условия (2.3) следует

(P AND H_k(T)) => H_k(P AND NOT BB), k ³ 0.

Тогда имеем

P AND wp(DO, T) = ($ k: k ³ 0: P AND H_k(T)) => ($ k: k ³ 0: H_k(P AND NOT BB)) = = wp(DO, P AND NOT BB).

Следовательно, (P AND wp(DO, T)) => wp(DO, P AND NOT BB).

Чтобы использовать аксиоматическую семантику с данным языком программирования для доказательства правильности программ или для описания формальной семантики, для каждого вида операторов языка должны быть определены аксиомы или правила логического вывода. С ними мы познакомимся в п. 2.3 «Верификация программ».

В аксиоматической семантике система (2.1) интерпретируется как набор аксиом в рамках некоторой формальной логической системы, в которой есть правила вывода и/или интерпретации определяемых объектов.

Для интерпретации системы функций (2.1) вводится понятие аксиоматического описания <S, A> - логически связанной пары понятий: S - сигнатура используемых в системе символов функций f₁, f₂, ..., f_m и символов констант (нульместных функциональных символов) c₁, c₂, ..., c_l, а A - набор аксиом, представленный системой. Предполагается, что каждая переменная x_i, i = 1, ..., k, и каждая константа c_i, i = 1, ..., l, используемая в A, принадлежит к какому-либо из типов данных t₁, t₂, ..., t_r, а каждый символ f_j, j = 1, ..., m, представляет функцию, типа: t_i1 t*_i2t*... _ik t_i0. Такое аксиоматическое описание получит конкретную интерпретацию, если будут заданы конкретные типы данных t_i = t_i', i = 1, ..., r, и конкретные значения констант c_i = c_i', i = 1, ..., l.

К. Хоaр построил аксиоматическое определение набора типов данных, которые потом Н. Вирт использовал при создании языка Паскаль.

Пример 2.6. Рассмотрим систему равенств:

УДАЛИТЬ(ДОБАВИТЬ(m,d)) = m,

ВЕРХ(ДОБАВИТЬ(m,d)) = d,

УДАЛИТЬ(ПУСТ) = ПУСТ,

ВЕРХ(ПУСТ) = ДНО,

где УДАЛИТЬ, ДОБАВИТЬ, ВЕРХ - символы функций, а ПУСТ и ДНО - символы констант, образующие сигнатуру этой системы. Пусть D, D1 и М - некоторые типы данных, такие, что m M, d D, ПУСТ M, ДНО D1, а функциональные символы представляют функции следующих типов:

УДАЛИТЬ: M M,

ДОБАВИТЬ:M, D M,

ВЕРХ:M D1.

Данная сигнатура вместе с указанной системой равенств, рассматриваемой как набор аксиом, образует аксиоматическое описание абстрактного типа данных, называемого магазином.

Зададим интерпретацию символов ее сигнатуры: D - множество значений, которые являются элементами магазина, M - множество состояний магазина, M = {d₁,d₂, ... ,d_n: d_i D, i = 1, ..., n, n ³ 0}, D1=D 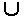{ДНО}, ПУСТ={}, а ДНО - особое значение (зависящее от реализации магазина), не принадлежащее D. Тогда указанный набор аксиом определяют свойства магазина.

При определении семантики полного языка программирования с использованием аксиоматического метода для каждого вида операторов языка должны быть сформулированы аксиома или правило логического вывода. Но определение аксиом и правил логического вывода для некоторых операторов языков программирования - очень сложная задача. Трудно построить «множество основных аксиом, достаточно ограниченное для того, чтобы избежать противоречий, но достаточно богатое для того, чтобы служить отправной точкой для доказательства высказываний о программах» (Э. Дейкстра).

Напрашивающимся решением такой проблемы является разработка языка, подразумевающего использование аксиоматического метода, т.е. содержащей только те операторы, для которых могут быть написаны аксиомы или правила логического вывода. К сожалению, подобный язык оказался бы слишком маленьким и простым что отражает нынешнее состояние аксиоматической семантики как науки.

Аксиоматическая семантика является мощным инструментом для исследований в области доказательств правильности программ, она также создает великолепную основу для анализа программ, как во время их создания, так и позднее. Однако ее полезность при описании содержания языков программирования весьма ограничена как для пользователей языка, так и для разработчиков компиляторов.