Денотационная семантика

Денотационная семантика - самый строгий широко известный метод описания значения программ. Она прочно опирается на теорию рекурсивных функций. Всестороннее рассмотрение денотационной семантики - длительное и сложное дело. Здесь мы познакомимся лишь с ее основными принципами.

Основной концепцией денотационной семантики является определение для каждой сущности языка некоего математического объекта и некоей функции, отображающей экземпляры этой сущности в экземпляры этого математического объекта. Поскольку объекты определены строго, то они представляют собой точный смысл соответствующих сущностей. Сама идея основана на факте существования строгих методов оперирования математическими объектами, а не конструкциями языков программирования. Сложность использования этого метода заключается в создании объектов и функций отображения. Название метода «денотационная семантика» происходит от английского слова denote (обозначать), поскольку математический объект обозначает смысл соответствующей синтаксической сущности.

Для введения в денотационный метод мы используем очень простую языковую конструкцию - двоичные числа. Синтаксис этих чисел можно описать следующими грамматическими правилами:

<двоичное_число> → 0; | 1; | <двоичное_число>0; | <двоичное_число>1.

Для описания двоичных чисел с использованием денотационной семантики и грамматических правил, указанных выше, их фактическое значение связывается с каждым правилом, имеющим в своей правой части один терминальный (основной) символ. Объектами в данном случае являются десятичные числа.

В нашем примере значащие объекты должны связываться с первыми двумя правилами. Остальные два правила являются, в известном смысле, правилами вычислений, поскольку они объединяют терминальный символ, с которым может ассоциироваться объект, с нетерминальным, который может представлять собой некоторую конструкцию.

Пусть область определения семантических значений объектов представляет собой множество неотрицательных десятичных целых чисел Nat. Это именно те объекты, которые мы хотим связать с двоичными числами. Семантическая функция М_b отображает синтаксические объекты в объекты множества N согласно указанным выше правилам. Сама функция М_b определяется следующим образом:

М_b('0') = 0, М_b('1')=1;

М_b(<двоичное_число> '0') = 2 × М_b(<двоичное_число>);

М_b(<двоичное_число> ‘1’) = + 2 × М_b(<двоичное_число>) + 1.

Мы заключили синтаксические цифры в апострофы, чтобы отличать их от математических цифр. Отношение между этими категориями подобно отношениям между цифрами в кодировке ASCII и математическими цифрами. Когда программа считывает число как строку, то прежде, чем это число сможет использоваться в программе, оно должно быть преобразовано в математическое число.

Пример 2.7. Описание значения десятичных синтаксических литеральных констант.

<десятичное_число> → 0|1|2|3|4|5|6|7|8|9;

| <десятичное_число> (0|1|2|3|4|5|6|7|8|9).

Денотационные отображения для этих синтаксических правил имеют следующий вид:

M_d(‘0') = 0, M_d('1') = 1, ,..., M_d('9') = 9;

М_d(<десятичное_число> '0') = 10 × М_d(<двоичное_число>);

М_d(<десятичное_число> ‘1’) = 10 × М_d(<десятичное_число>) + 1;

…

М_d(<десятичное_число> '9') = 10 × М_d(<десятичное_число>) + 9.

Денотационную семантику программы можно определить в терминах изменений состояний идеального компьютера. Подобным образом определялись операционные ceмантики, приблизительно так же определяются и денотационные. Правда, для простоты они определяются только в терминах значений всех переменных, объявленных в программе. Операционная и денотационная семантики различаются тем, что изменения состояний в операционной семантике определяются запрограммированными алгоритмами, а в денотационной семантике они определяются строгими математическими функциями. Пусть состояние s программы определяется следующим набором упорядоченных пар: {<i₁, v₁>, <i₂, v₂>, …, <i_n, v_n>}.

Каждый параметр i является именем переменной, а соответствующие параметры v являются текущими значениями данных переменных. Любой из параметров v может иметь специальное значение undef, указывающее, что связанная с ним величина в данный момент не определена.

Пусть VARMAP - функция двух параметров, имени переменной и состояния программы. Значение функции VARMAP(i_k, s) равно v_k (значение, соответствующее параметру i_k в состоянии s).

Большинство семантических функций отображения для программ и программных конструкций отображают состояния в состояния. Эти изменения состояний используются для определения смысла программ и программных конструкций. Отметим, что такие языковые конструкции, как выражения, отображаются не в состояния, а в величины.

Выражения являются основой большинства языков программирования. Более того, мы имеем дело только с очень простыми выражениями. Единственными операторами являются операторы + и ×; выражения могут содержать не более одного оператора; единственными операндами являются скалярные переменные и целочисленные литеральные константы; круглые скобки не используются; значение выражения является целым числом. Ниже следует описание этих выражений в форме БНФ:

<выражение> → <десятичное_число>| <переменная>

| <двоичное_выражение>

<двоичное_выражение> → <выражение_слева><оператор>

<выражение_справа>

<оператор> → + | ×

Единственной рассматриваемой нами ошибкой в выражениях является неопределенное значение переменной. Разумеется, могут появляться и другие ошибки, но большинство из них зависят от машины. Пусть Z - набор целых чисел, a error - ошибочное значение. Тогда множество Z 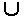{error} является множеством значений, для которых выражение может быть вычислено.

Ниже приведена функция отображения для данного выражения Е и состояния s. Символ º обозначает равенство по определению функции.

M_e(<выражение>, s) º