Краткое введение в исчисление высказываний
Аксиоматическая семантика основана на математической логике. Будем называть предикат, помещенный в программу высказыванием (иногда употребляют термин утверждение). Высказывание, непосредственно предшествующее оператору программы, описывает ограничения, наложенные на переменные в данном месте программы. Высказывание, следующее непосредственно за оператором программы, описывает новые ограничения на те же (а возможно, и другие) переменные после выполнения оператора.
Обычно термин высказывание используется для логических переменных, принимающих одно из двух значений F и Т, которые представляют понятия «ложь» и «истина». На значениях типа «логический» определены пять операций: отрицание: (NOT b), конъюнкция: (b AND с), дизъюнкция: (b OR с), импликация: (b 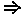 с), равенство: (b = с). Высказывания строятся по следующим правилам.
с), равенство: (b = с). Высказывания строятся по следующим правилам.
1.F и Т – высказывания.
2.Идентификаторы (непустая последовательность букв и цифр, начинающаяся с буквы) являются высказываниями.
3.Если b – высказывание, то (NOT b) высказывание.
4.Если b и с – высказывания, то (b OR с), (b AND с), (b = с), (b 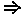 с) – также высказывания.
с) – также высказывания.
Вычисление постоянных высказываний, содержащих в качестве операндов только константы, имеет три определяемых структурой высказывания E случая: E без операций, E с одной операцией, E с более чем одной операцией.
1.Значение Т есть Т, значение F есть F.
2.Значения (NOT b), (b AND с), (b OR с), (b 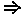 с), (b = с), где b и с – константы F и Т в любой комбинации, определяются по таблице, называемой таблицей истинности.
с), (b = с), где b и с – константы F и Т в любой комбинации, определяются по таблице, называемой таблицей истинности.
| b | c | NOT b | b AND с | b OR с | b 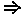 с с
| b = с |
| F | F | T | F | F | T | T |
| F | T | T | F | T | T | F |
| T | F | F | F | T | F | F |
| T | T | F | T | T | T | T |
3.Значение постоянного высказывания, содержащего более чем одну операцию, получается последовательным применением таблицы истинности к подвысказываниям этого высказывания и заменой подвысказываний на их значения до тех пор, пока высказывание не сведется к F или Т.
Состояние s – это функция из множества идентификаторов в множество значений F и Т. Высказывание E определено в состоянии s, если каждый идентификатор из E встречается в s. s(E) – значение E в состоянии s – получаемое заменой всех вхождений идентификаторов b в высказывание E на их значения s(b) и вычислением получившегося постоянного высказывания.
Тавтология – высказывание, истинное в любом состоянии, в котором оно определено.
Высказывание выражает, или описывает, множество состояний, в котором оно истинно.
Правила старшинства операций:
1.Последовательность одноименных операций вычисляется слева направо.
2.Порядок вычислений различных между собой и смежных в записи высказывания операций определяется списком: NOT,AND,OR, 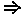 , =.
, =.
Вычисление высказываний редко бывает самоцелью. Чаще необходимо манипулировать ими, чтобы вывести «эквивалентные», но более простые высказывания.
Высказывания Е1 и Е2 эквивалентны, если и только если Е1 = Е2 есть тавтология. Здесь Е1 ~ Е2 эквивалентность.
1. Законы коммутативности: (Е1  Е2) = (Е2
Е2) = (Е2  Е1),
Е1),  - обозначает операции = , AND, OR.
- обозначает операции = , AND, OR.
2. Законы ассоциативности: (Е1  Е2)
Е2)  Е3 = Е1
Е3 = Е1  (Е2
(Е2  Е3),
Е3),  - обозначает операции AND, OR.
- обозначает операции AND, OR.
3. Законы дистрибутивности: (Е1  Е2) Å Е3 = (Е1 Å Е3)
Е2) Å Е3 = (Е1 Å Е3)  (Е2 Å Е3),
(Е2 Å Е3),  и Å - обозначают операции AND, OR.
и Å - обозначают операции AND, OR.
4. Законы де Моргана: NOT (Е1  Е2) = NOT Е1 Å NOT Е1),
Е2) = NOT Е1 Å NOT Е1),  и Å- обозначают операции AND, OR.
и Å- обозначают операции AND, OR.
5. Закон отрицания: NOT(NOTЕ1) = Е1.
6. Закон исключенного третьего: Е1 OR NOT Е1 = Т.
7. Закон противоречия: Е1 AND NOT Е1 = F.
8. Закон импликации: : (Е1 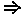 Е2) = NOT Е1 OR Е2.
Е2) = NOT Е1 OR Е2.
9. Закон равенства: (Е1 = Е2) = (Е1 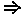 Е2) AND(Е2
Е2) AND(Е2 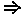 Е1).
Е1).
10.Законы упрощенияOR: Е1OR Е1 = Е1, Е1OR (Е1AND Е2) = Е1,Е1 OR Т = Т, Е1 OR F = Е1.
11.Законы упрощенияAND: Е1AND Е1 = Е1, Е1AND (Е1OR Е2) = Е1,Е1 AND Т = Е1, Е1 AND F = F.
12.Закон тождества Е1 = Е1.
Для вычисления высказываний используют правила подстановки и транзитивности.
Правило постановки: Если е1 = е2 – эквивалентность, а Е(х) – высказывание, записанное как функция от одного из своих идентификаторов х. Тогда Е(е1) = Е(е2) и Е(е2) = Е(е1) эквивалентности.
Правило транзитивности: Если е1 = е2 и е2 = е3 – эквивалентности, то е1 = е3 - эквивалентности.
Для формулирования развернутых высказываний используются кванторы.
Квантор существования ($i: m  i < n: Ei).
i < n: Ei).
Квантор всеобщности ("i: m  i < n: Ei) = NOT($i: m
i < n: Ei) = NOT($i: m  i < n: NOTEi)
i < n: NOTEi)
Множество значений, удовлетворяющих m  i < n, называется областью значений квантифицированной переменной i.
i < n, называется областью значений квантифицированной переменной i.
Вхождение идентификатора i в предикат называется связанным, если оно находится в области действия квантора "i или $i, и свободным в противном случае.
В одном и том же выражении один и тот же идентификатор не может быть как связанным, так и свободным и идентификатор не может быть связан двумя различными кванторами.
Дата добавления: 2015-07-18; просмотров: 1235;
